5
Объяснение:
По расширенной теореме синусов радиус описанной окружности равен
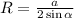 , где а - известная сторона, α - угол противолежащий данной стороне.
, где а - известная сторона, α - угол противолежащий данной стороне.
Найдем угол, противолежащий данной стороне. По теореме о сумме углов треугольника в Евклидовой геометрии получаем
45°+75°+α=180°
α=180°-75°-45°
α=60°
Подставим в формулу, нахождения радиуса описанной окружности
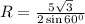
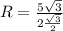
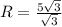
R=5
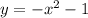
а < 0 ⇒ ветви направлены вниз
-х²-1 ⇒ график функции сдвигается вниз по оси ординат на 1
Подходящий график: Б
2.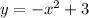
а < 0 ⇒ ветви направлены вниз
-х²+3 ⇒ график функции сдвигается вверх по оси ординат на 3
Подходящий график: Г
3.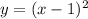
а > 0 ⇒ ветви направлены вверх
(х-1)² ⇒ график функции сдвигается вправо по оси абсцисс на 1
Подходящий график: Д
4.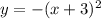
а < 0 ⇒ ветви направлены вниз
(x+3)² ⇒ график функции сдвигается влево по оси абсцисс на 3
Подходящий график: А
5.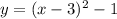
а > 0 ⇒ ветви направлены вверх
(x-3)²-1 ⇒ график функции сдвигается вправо по оси абсцисс на 3, да ещё вниз по оси ординат на 1
Подходящий график: Е
6.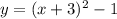
а > 0 ⇒ ветви направлены вверх
(x+3)²-1 ⇒ график функции сдвигается влево по оси абсцисс на 3, да ещё вниз по оси ординат на 1
Подходящий график: В
1) Найдем противолежащий против этой стороны угол:
c = 180°-a-b = 180°-120° = 60°
2)Теорема синусов:
a/sin a = b/sin b = c/sin c = 2R
2R = 5✓3/sin60° = 5✓3•2/✓3 = 10
R = 5