Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру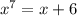 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Пусть скорость первого рабочего х, тогда скорость другого рабочего у. Работая вместе, они выполняют работу, равную 1. На это они тратят время 1/(x+y)=12ч
Если же они будут работать по очереди, то затратят 1/(2х)+1/(2у)=25ч
Решаем систему уравнений, х=1/30 и у=1/20 или наоборот.
Это значит, что один рабочий закончил бы всю работу за 30 ч, другой за 20.