Корней нет
Если проходите комплексные числа, то решение
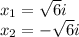
Объяснение:
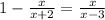 перенесем выражение с неизвестной в правую часть и поменяем местами
перенесем выражение с неизвестной в правую часть и поменяем местами
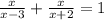 приведем к общему знаменателю
приведем к общему знаменателю
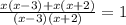 домножим обе части на (х-3)(х+2) и сократим в левой части, добавив условие (х-3)(х+2) ≠0 ⇔ х ≠3 и х≠-2
домножим обе части на (х-3)(х+2) и сократим в левой части, добавив условие (х-3)(х+2) ≠0 ⇔ х ≠3 и х≠-2
x(х-3) + x(х+2) = (х-3)(х+2), раскроем скобки и сгруппируем
2х^2 - x = х^2 - x - 6, перенесем из правой части выражения содержащие переменную в левую со знаком минус и сгруппируем:
х^2 = -6
Корней нет
Если проходите комплексные числа, то решение
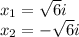
a/(a^2-b^2)-a/(a^2+ab)=2*b/((a-b)*(a+b))=2корней из 6
сначала в знаменателе вынесем общий множитель за скобки
a/(a*(a-b))-a/(a*(a-b))
приведем к общему знаменателю а*(a-b)*(a+b),дополнительный множитель для первой дроби (a+b) , дополнительный множитель для второй дроби (a-b)
получим
(a*(a+b)-a*(a-b)) / (a*(a-b)*(a+b))
в числителе раскрываем скобки
(а^2+ab-a^2+ab) / (a*(a-b)*(a+b))
в числители приводим подобные слагаемые a^2 -a^2=0 ab+ab=2ab,получим
2ab / (a*(a-b)*(a+b))
сократим на а числитель и знаменатель
получим 2 b / (a-b)*(a+b)
в знаменателе свернем по формуле разность квадратов и получим 2 b / (a^2-b^2)
подставим числа, в числителе будет 2 корней из 6, в знаменателе 1
ответ будет 2корней из 6