а) 3 прямые имеют наибольшее число точек пересечения 3 ,
б) 4 прямые - 6 точек пересечения ,
в) 5 прямых - 10 точек пересечения ,
г) n прямых - \frac{n(n-1)}{2}
2
n(n−1)
точек пересечения .
Решение. Заметим, что наибольшее число точек попарных пересечений получается, если каждая прямая пересекается с каждой и при этом никакие три прямые не пересекаются в одной точке. В этом случае количество точек попарных пересечений равно количеству пар прямых из данного множества n прямых. Как мы знаем, это число равно \frac{n(n-1)}{2}
2
n(n−1)
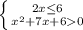
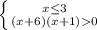
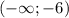 и
и 
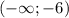 и
и ![(-1;3]](/tpl/images/0188/5648/df8ed.png)

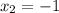
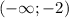 и
и 
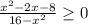
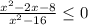
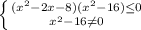
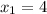

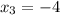
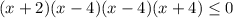
![(-4;-2]](/tpl/images/0188/5648/eac16.png)
ответ: .
.
Объяснение:
Решаем по формуле полной вероятности.
Событие А=(из 2 урны вынули белый шар ) .
Гипотеза Н1=(из 1 урны вынули белый шар и переложили во 2 урну) , Р(Н1)=3/7 .
Гипотеза Н2=(из 1 урны вынули черый шар и переложили во 2 урну) , Р(Н2)=4/7 .
Условные вероятности: Р(А/Н1)=6/13 , Р(А/Н2)=5/13 .