![\sqrt{\frac{2x-1}{3x-2}}\leq 3\Leftrightarrow \frac{2x-1}{3x-2}\leq 9\Leftrightarrow \\\frac{2x-1}{3x-2}\geq 0\Rightarrow x\in \left ( - \infty;\frac{1}{2}\right ]\cup \left ( \frac{2}{3};+\infty \right )\\\Leftrightarrow \frac{17-25x}{3x-2}\leq 0\Rightarrow x\in \left ( -\infty;\frac{2}{3} \right )\cup \left [\frac{17}{25};+\infty \right )\\x\in \left ( -\infty;\frac{1}{2} \right ]\cup \left [\frac{17}{25};+\infty \right )](/tpl/images/1050/1832/05b9a.png)
При a=-2 неравенство ax^2-(8+2a^2)x+16a>0 не имеет решений
Объяснение:
Выражение слева при а≠0 представляет собой параболу (при а=0 - решение есть).
Определим, при каких а у=ax^2-(8+2a^2)x+16a пересекает ось ОХ
Найдем дискриминант для ax^2-(8+2a^2)x+16a=0
D=(8+2а²)²-4а*16a=(8+2а²)²-(8а)²=(8+2а²-8а)(8+2а²+8а)=4(а-2)²(а+2)²=4(а²-4)²
D≥0 при любых значениях а, т. е. точки пересечения(хотя бы одна) с осью ОХ есть всегда.
Парабола будет лежать ниже оси ОХ в случае, когда а<0(ветви вниз направлены) и D=0(одна точка пересечения с осью ОХ)
4(а²-4)²=0; а²-4=0; a=-2
Объяснение:
ОДЗ: х є (-∞,½]U[⅔,+∞)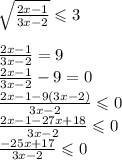
х є (-∞,⅔)U[17/25,+∞), х є (-∞,½]U[⅔,+∞)
x є (-∞,½]U[17/25,+∞)