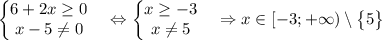
Интегрирование — это одна из двух основных операций в математическом анализе. В отличие от операции дифференцирования, интеграл от элементарной функции может не быть элементарной функцией. Например, из теоремы Лиувилля следует, что интеграл от {\displaystyle e^{x^{2}}}e^{x^2} не является элементарной функцией. Таблицы известных первообразных оказываются часто очень полезны, хотя сейчас и теряют свою актуальность с появлением систем компьютерной алгебры. На этой странице представлен список наиболее часто встречающихся первообразных.
Объяснение:
Интегрирование — это одна из двух основных операций в математическом анализе. В отличие от операции дифференцирования, интеграл от элементарной функции может не быть элементарной функцией. Например, из теоремы Лиувилля следует, что интеграл от {\displaystyle e^{x^{2}}}e^{x^2} не является элементарной функцией. Таблицы известных первообразных оказываются часто очень полезны, хотя сейчас и теряют свою актуальность с появлением систем компьютерной алгебры. На этой странице представлен список наиболее часто встречающихся первообразных.
Объяснение:
Объяснение:
1) Поменять порядок слагаемых или множителей:
2) Разделите функцию на части:
2) Найдите все значения, для которых подкоренное выражение положительно или 0. Область определения - все действительные числа. Найдите все значения, для которых знаменатель отличен от 0:
х принадлежит R
х принадлежит R \ {5}
х принадлежит R
х принадлежит R
3) Найти пересечение:
х принадлежит [-3;5) (знак на фото) (5; до +бесконечность)