Задание 1.
1) 15ab+10bc= 5b(3a+2c).
2)3x²+6xy+3y²= 3(x²+2xy+y²)= 3(x+y)².
3)6x(x-1)-(1-x)= 6x(x-1)+(x-1)= (x-1)(6x+1).
4)3a³+3= 3(a³+1)= 3(a+1)(a²-a+1).
5) 2a-2b+a²-b²= 2(a-b)+(a-b)(a+b)= (a-b)(2+a+b).
6)-3x(x+3)+x³+27= -3x(x+3)+(x+3)(x²-3х+9)= (х+3)(-3х+х²-3х+9)= (х+3)(х²-6х+9)=(х+3)(х-3)².
Задание 2.
(43²-17²):(43²-2•43•17+17²)= ((43-17)(43+17)) ÷ (43-17)²= 26•60÷26²= 60÷26=30/13= 2 4/13 (две целых четыре тринадцатых).
P.S. Возможно Вы неправильно списали с условия во втором задании, пересмотрите условие, я заменила "+" на знак умножения.
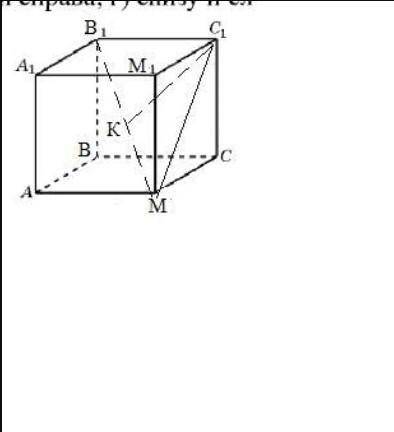
Рассчитай расстояние вершины куба до диагонали куба, которая не проходит через эту вершину, если ребро куба — 45 см
Объяснение:
Пусть АВСМА₁В₁С₁М₁-куб, АВ=45см. Все грани равные квадраты.Расстоянием от вершины С₁ до диагонали В₁М будет длина перпендикуляра С₁К.
Найдем диагональ квадрата по т. Пифагора ⇒ 45√2 см.
Найдем диагональ куба d²=45²+45²+45² , d²=3*45² , d=45√3 см.
ΔМВ₁С₁- прямоугольный, т.к. проекция М₁С₁⊥ В₁С₁ , то и наклонная МС₁⊥В₁С₁ по т. о трех перпендикулярах. Используя формулу площади треугольника :
S(В₁С₁М)=1/2*В₁С₁*С₁М или S(В₁С₁М)=1/2*В₁М*С₁К ⇒
S(В₁С₁М)=1/2*45*45√2 , подставим во вторую формулу, получим :
1/2*45*45√2=1/2*45√3*С₁К или С₁К=(45√2)/√3=(45√6)/3=15√6 (см)
Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби {\displaystyle \pm {\frac {m}{n}}}{\displaystyle \pm {\frac {m}{n}}}, где {\displaystyle m,n}m,n — натуральные числа. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Иррациональные числа
ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — {\displaystyle e^{\pi }}e^{\pi } и π
Другими словами, множество иррациональных чисел есть разность {\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} }{\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} } множеств вещественных и рациональных чисел.
О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа {\displaystyle {\sqrt {2}}}{\sqrt {2}}[1].
К числу иррациональных чисел относятся отношение π окружности круга к его диаметру, число Эйлера e, золотое сечение φ и квадратный корень из двух[2][3][4]; на самом деле все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.
Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби. Следствием доказательства Кантора является то, что действительные числа неисчислимы, а рациональные счетны, отсюда следует, что почти все действительные числа иррациональны[5].
1) 15ab + 10bc = 5b(3a + 2c)
2) 3x² + 6xy + 3y² = 3(x² + 2xy + y²) = 3(x + y)²
3) 6x(x - 1) - (1 - x) = 6x(x - 1) + (x - 1) = (x - 1)(6x + 1)
4) 3a³ + 3 = 3(a³ + 1) = 3(a + 1)(a² - a + 1)
5) 2a - 2b + a² - b² = (2a - 2b) + (a² - b²) = 2(a - b) + (a - b)(a + b) =
= (a - b)(2 + a + b)
6) - 3x(x + 3) + x³ + 27 = - 3x(x + 3) + (x³ + 3³) = - 3x(x + 3) + (x + 3)(x² - 3x + 9) = (x + 3)(- 3x + x²- 3x + 9) = (x + 3)(x² - 6x + 9) = (x + 3)(x - 3)²
Вычислить :