Объяснение:
Линейное уравнение – уравнение, сводящееся к виду ax+b=0, где a≠0,b – числа. Линейное уравнение всегда имеет единственное решение x=−ba. Квадратное уравнение – уравнение, сводящееся к виду ax2+bx+c=0, где a≠0,b,c – числа. Выражение D=b2−4ac называется дискриминантом квадратного уравнения. Квадратное уравнение может иметь не более двух корней: ∙ если D>0, то оно имеет два различных корня и x1=−b+D2aиx2=−b−D2a ∙ если D=0, то оно имеет один корень (иногда говорят, что два совпадающих) x1=x2=−b2a ∙ если D<0, то оно не имеет корней. ▸ Теорема Виета для квадратного уравнения: Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения x1+x2=−ba а произведение x1⋅x2=ca ▸ Если квадратное уравнение: ∼ имеет два корня x1 и x2, то ax2+bx+c=a(x−x1)(x−x2). ∼ имеет один корень x1 (иногда говорят, что два совпадающих), то ax2+bx+c=a(x−x1)2. ∼ не имеет корней, то квадратный трехчлен ax2+bc+c никогда не может быть равен нулю. Более того, он при всех x строго одного знака: либо положителен, либо отрицателен. ▸ Полезные формулы сокращенного умножения: x2−y2=(x−y)(x+y)(x+y)2=x2+2xy+y2(x−y)2=x2−2xy+y2 Ознакомиться с полной теорией
Объяснение:
у=х-4 х€[-1; 7]
k=1>0 ===> y(x) - возрастающая
функция.
а1.
Наименьшее значение функция
принимает в левой крайней точ
ке заданного отрезка х=-1 :
у(-1)=-1-4=-5
а2.
Наибольшее значение функция
принимает в правой крайне точ
ке заданного отрезка х=7 :
у(7)=7-4=3
б1.
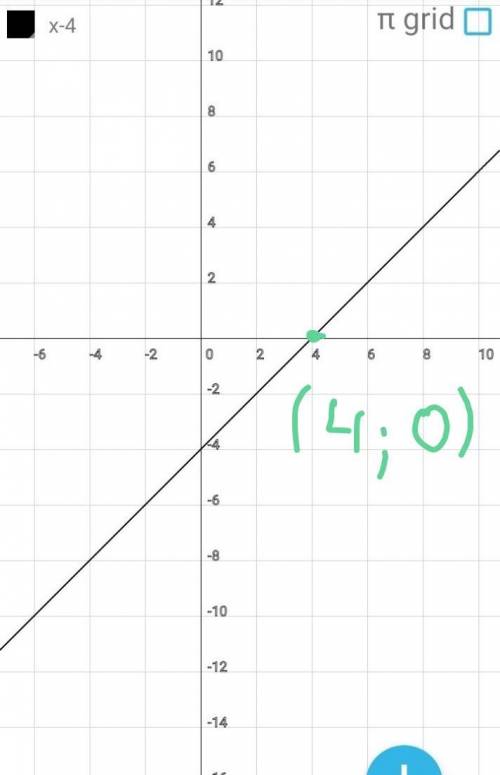
Если у=0, то:
0=х-4
-х=-4
х=4
Значение у=0 функция достига
ет в точке сабсциссой, равной 4.
б2.
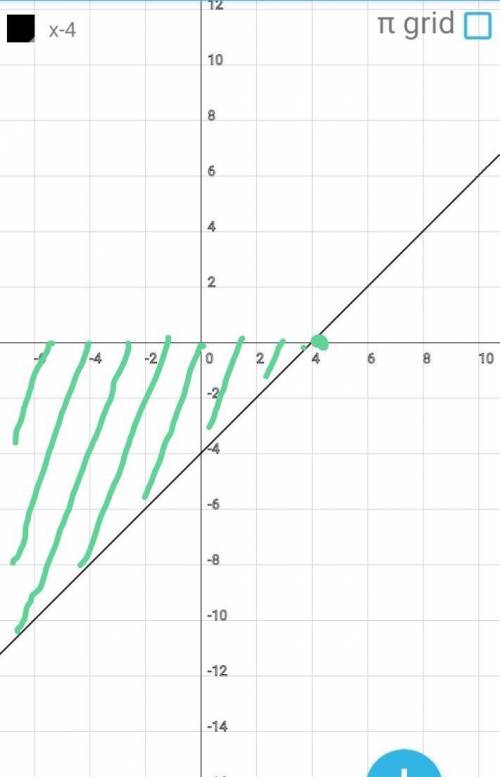
х-4<0
х<4
Вывод:
функция принимает отрицтаель
ные значения у<0 при
х€(-оо; 4).
Строим график функции
у=х-4
Составим и заполним таб
личку: достаточно двух точек,
так как графиком линейной
функции является прямая ли
ния.
х -1 3
у -5 -1

ответ: a=-1 ; a=2
Объяснение:
2(a-2)x²+a(a+1)x+6=0
По теореме Виета произведение корней равно :
6/(2(a-2)) = 3/(a-2)
Поскольку произведение корней должно быть целым , то
a-2 - рациональное число a-2 = p/q p и q взаимно простые p-целое число , q- натуральное число
3/(a-2) = 3/ (p/q) = 3*q/p
Поскольку p и q взаимно простые
p=+-3 ; +-1
a-2=p/q
a*(a+1) = (p/q +2)*(p/q +3)
2*p*x^2/q + (p/q +2)*(p/q +3)*x +6=0
Умножим обе части равенства на q^2
2*p*q*x^2 + (p+2q)*(p+3q) +6*q^2=0
Тогда по теореме Виета - cумма корней равна
N= -(x1+x2) = (p+2q)*(p+3q)/(2*p*q)
1) p=1
N = (1+2q)*(1+3q)/2q = (1+3q)/2q + 1+3q = (1+q)/2*q + 2+3q
Таким образом : 1+q делится на 2*q
1+q =2*q*n n ,q - натуральные числа (1+q - так же натуральное число соответственно)
1 = q* (2n-1 )
q=1
2) p=-1
(2q-1)*(3q-1)/(-2*q) = (2q-1) *(1-3q)/2q = 1-3q + (3q-1)/2q = 2-3q +(q-1)/2q
q-1 делится на 2q
q-1 = 2*q*n n-целое , q- натуральное
1= q* ( 1-2n)
q=1
Таким образом : a12= +-1/1 = +-1 ( кандидаты на a )
3) p= 3
(3+2q)*(3+3q)/6*q = ( 6*q*(1+q) + 9*(1+q) ) /6q = 1+q +(3+3q) /2q =
(q+3)/2q + 2+q
q+3 делится на 2q
q+3 =2*q*n q,n- натуральные
3= q*(2n-1)
q=3 ; 1 a=3/3=1=a1 ; a3= 3/1= 3
4) p=-3
(2q-3)*(3q-3)/(-6q) = (2q-3)* (1-q)/2q = 1-q + (3q-3)/2*q = 2-q +(q-3)/2q
q-3 делится на 2q
q-3= 2*q*n n-целое , q- натуральное
3= q*(1-2n)
q=3 ; 1 ( q=3 подходит тк 2-q +(q-3)/2q = 2-3=-1
a= -3/3=-1 =a2 ; a4= -3/1= -3
Таким образом : a=+-1 ; +-3 единственные кандидаты на уравнение с целочисленными корнями
Проверяем :
a=1
-2*x^2 +2*x+6=0
x^2-x-3=0
D =1+12=13 - не полный квадрат. ( не подходит)
a=-1
-6*x^2 +6=0
6=6*x^2
x^2=1
x=+-1
a=-1 (подходит)
a=3
2*x^2 +12*x +6=0
x^2+6*x+3=0
D=36-12=24 - не полный квадрат ( не подходит)
a=-3
-10*x^2 +6*x +6 =0
5*x^2-3*x-3=0
D= 9+60=69 - не подходит.
ответ : a=-1 ( казалось бы!)
Но мы кое что забыли !
Рассмотрим случай a=2 , в этом случае наше уравнение становится линейным :
6*x+6=0
x=-1 , то есть a=2 подходит .
Случай же ,когда D=0 соответствует общему случаю .
Только сумма корней по теореме Виета равна 2*x0 , а произведение xo^2 ( корень второй кратности равный x0).
Так что в этом моменте все в порядке