Приймемо роботу за 1. х годин треба першому, в годин треба другому. перший за часом зробить 1 / х частина роботи, другий 1 / у. Разом за 6 годин вони зроблять (1 / х + 1 / у) * 6 або всю роботу; рівняння (1 / х + 1 / у) * 6 = 1
за 6 годин перший зробить 6 / г частину роботи, другий за 4 години 4 / в частина роботи, разом 6 / х + 4 / в або 0,8 роботи (80%); рівняння 6 / х + 4 / в = 0,8.
Об'єднати в систему:
6 / х + 6 / в = 1
6 / х + 4 / в = 0,8 віднімемо друге рівняння з першого
2 / в = 0,2 у = 10 (годин)
Підставами в перше рівняння і знайдемо х
6 / х + 6/10 = 1 6 / х = 4/10 х = 15 (годин)
Відповідь: першому треба 15 год, другого - 10 год.
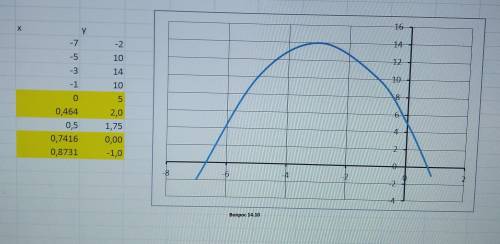
14.10
1) f(0)=5; f(0,464)=2; f(-6,873)=-1
2) ) f(-6,742)=0; ) f(0,7416)=0
Функция положительная при -6,742< х<0,7416
3) Вершина параболы при х= -3 Ось симметрии х=-3
4) наибольшее значение f(-3)=14
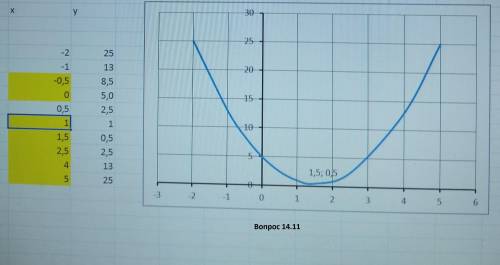
14.11
1) Вершина параболы при х= 1,5 Ось симметрии х=1,5
2) наименьшее значение f(1,5)=0,5 множества значений f(х)≥0,5
3) Промежутки возрастания х>1,5
Убывания х< 1,5
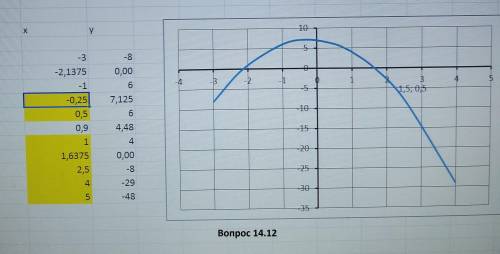
14.12
1) Вершина параболы при х= -0,25 Ось симметрии х=-0,25
2) наибольшее значение f(-0,25)=7,125
множества значений f(х)≤ 7,125
Промежутки возрастания х<-0,25
Убывания х>-0,25
Объяснение:
(х + 2 )² = 2 (х + 2) + 3
Расписываем квадрат суммы в левой части и раскрываем скобки во второй части уравнения
х² + 2*2*х + 2² = 2х +4 +3
х² + 4х + 4 =2х +7
Перенесем все части в левую сторону:
х² + 4х +4 -2х -7 = 0
Сложим подобные члены:
х² +2х -3 = 0
Решим квадратное уравнение с дискриминанта:
D = b² - 4 *a*c = 2² - 4 *1 * (-3) = 4 + 12 = 16
√D = 4
х1 = (-2 -4) : 2= -6 :2 = -3;
х2= (-2+4) : 2 = 2:2 = 1
ответ: корни уравнения х1 = -3; х2 = 1.