1)
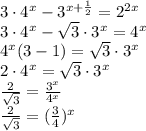
Возьмём логарифм по основанию 3/4 от обеих частей.
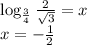
2)
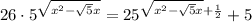
Заменим 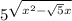 на t.
на t.
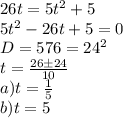
а)
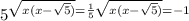
Решений нет.
б)
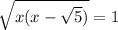
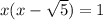
Решив квадратное уравнение, получаем:
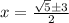
Так как √5 < 3, то один из корней меньше нуля.
ответ: 1.
у = 0,75х + 3
Объяснение:
На рисунке изображена линия. Значит, это - график линейной функции.
Уравнение графика линейной функции:
у = kx + b,
где k - угловой коэффициент (или, по-другому, - тангенс угла наклона данной прямой к оси х);
b - это, взятая с соответствующим знаком, точка на оси у, которую пересекает данная прямая.
1) Находим k.
Для этого выбираем любой треугольник, где график точно проходит по узлам и противолежащий катет (у) делим на прилежащий катет (х).
Хорошие точки на этом графике - это точки пересечения с осями х = - 4, у = 3. Так как функция возрастаем, то, не обращая внимания на знаки, делим 3 на 4, получаем 0,75.
k = 0,75.
2) Данный график пересекает ось у в точке у = 3; значит b = 3.
3) Мы получили уравнение:
у = 0,75х + 3
ПРОВЕРКА
Проверку делаем по 2 точкам, т.к. для прямой этого достаточно.
Если х = -4, то у = 0,75 · (-4) + 3 = -3 + 3 = 0 - правильно; на графике именно так;
если х = 0, то у = 0,75 · 0 + 3 = 3 - тоже правильно, т.к. и на графике при х = 0 у = 3.
ответ: у = 0,75х + 3
В равностороннем треугольнике все стороны равны и каждый угол равен 60°. Также в равностороннем треугольнике все высоты равны, так что найдём любую. Проводим высоты. В равностороннем треугольнике высота является медианой и биссектрисой. Таким образом высота делить сторону длиной
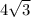
На два равны отрезка. Получим прямоугольный треугольник (так как у гол между сторону и высотой, проведённой к данной стороне равен 90°), у которого катет и гипотенуза равны
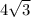
И
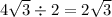
Соответственно, пусть высота равна h, тогда по теореме Пифагора
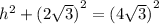
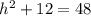
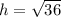
h = 6
ответ: 6
3*4^x - 3^(x + 1/2) = 2^2x
(a^m)^n = a^mn
a^0 = 1 (a≠0)
3*4^x - 3^(x + 1/2) = 4^x
2*4^x = 3^(x + 1/2)
2 = 4^1/2
4^(x + 1/2) = 3^(x + 1/2)
(3/4)^(x + 1/2) = 1
x + 1/2 = 0
x = -1/2
26*5^(√(x^2 - √5*x)) = 25^(√(x^2 - √5*x) + 1/2) + 5
26*5^(√(x^2 - √5*x)) = 5^2(√(x^2 - √5*x) + 1/2) + 5
26*5^(√(x^2 - √5*x)) = 5*5^2(√(x^2 - √5*x)) + 5
5^(√(x^2 - √5*x)) = t > 0
26t = 5t² + 5
5t² - 26t + 5 = 0
D = 26^2 - 4*5*5 = 676 - 100 = 576 = 24^2
t12 = (26 +- 24)/10 = 5 1/5
1. t1 = 5
5^(√(x^2 - √5*x)) = 5
√(x^2 - √5*x) = 1
x^2 - √5*x = 1
x^2 - √5*x - 1 = 0
D = √5² + 4 = 9
x12 = (√5 +- 3)/2
x1 = (√5 + 3)/2 > 0
x2 = (√5 - 3)/2 < 0 (√5 < 3) да корень по условию
2. t1 = 1/5
5^(√(x^2 - √5*x)) = 1/5
√(x^2 - √5*x) = -1
корень четной степени на поле действительных чисел не может быть меньше 0
решений действительных нет
ответ один корень (√5 - 3)/2