Чтобы доказать, что функция f(x) является первообразной для функции f(x) на промежутке (-∞; +∞), мы должны показать, что производная функции f(x) равна функции f(x).
Прежде чем начать, давайте определим, что такое первообразная функция. Первообразная функция, или интеграл, обратная операции дифференцирования. Если функция f(x) имеет первообразную функцию F(x), то производная от F(x) равна f(x).
Теперь решим задачу.
Чтобы доказать, что f(x) является первообразной для f(x), мы должны показать, что производная функции f(x) равна f(x). Давайте возьмем производную от f(x) и проверим.
f(x) = 50!
Для начала, нужно выразить факториал 50!. Факториал числа n обозначается n! и равен произведению всех натуральных чисел от 1 до n.
50! = 50 × 49 × 48 × ... × 3 × 2 × 1
Теперь возьмем производную от f(x). Обратите внимание, что функция f(x) - это функция одной переменной, поэтому мы берем производную по переменной x:
f'(x) = d(50!)/dx
Согласно правилам дифференцирования, производная от константы (как 50! в данном случае) равна нулю. Поэтому производная от 50! равна 0:
f'(x) = 0
Теперь сравним производную f'(x) с функцией f(x):
f'(x) = 0
f(x) = 50!
Мы видим, что производная функции f(x) равна функции f(x), поэтому можем сделать вывод, что функция f(x) является первообразной для функции f(x) на промежутке (-∞; +∞).
Надеюсь, это решение понятно. Если у вас есть еще вопросы или нужно дополнительное объяснение, пожалуйста, дайте знать!
Функция F(x) является первообразной для функции f(x) , если выполняется равенство: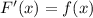 .
.
В обоих примерах F(x) явл. первообразной функцией для f(x) .