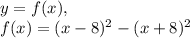
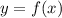— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 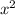(не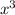 
, не 
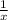, не 
и не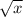 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид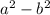 
, где 
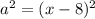, и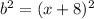 
. Формула «разность квадратов» раскрывается так: 
.
.
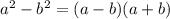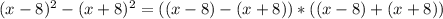
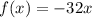, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
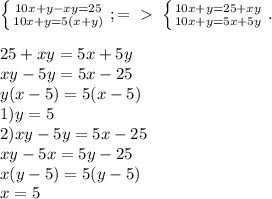
Объяснение:
y'=6x^2-18x+12, 6x^2-18x+12=0, x^2-3x+2=0, корни ур-я x=1 и x=2,
на числ. прямой отмечаем точки 1 и 2 и знаки производной,
+ 1 - 2 + , поизводная меняет в т.1 знак с (+) на (-), х=1 max, в т. 2 с (-) на (+) , х=2 min, чтобы найти значения в точках экстремума надо подставить эти значения в функцию и подсчитать