Для того чтобы разложить на множители выражение вида 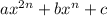 , где
, где 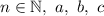 — числа, достаточно решить квадратное уравнение
— числа, достаточно решить квадратное уравнение 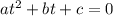 , где
, где 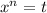 , и применить формулу разложения:
, и применить формулу разложения: 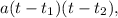 где
где 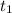 и
и 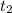 — корни данного квадратного уравнения, после чего нужно сделать обратную замену.
— корни данного квадратного уравнения, после чего нужно сделать обратную замену.
Итак, имеем биквадратный трехчлен 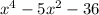 . Сделаем подходящую замену:
. Сделаем подходящую замену: 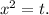 Получили квадратный трехчлен
Получили квадратный трехчлен 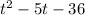 .
.
Решим уравнение 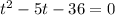 при теоремы Виета:
при теоремы Виета:
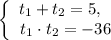
Получили корни: 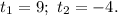
Подставим полученные корни в формулу: 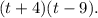 Сделаем обратную замену:
Сделаем обратную замену: 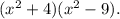 Применим формулу разности квадратов
Применим формулу разности квадратов 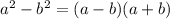 и получаем окончательное разложение данного биквадратного трехчлена:
и получаем окончательное разложение данного биквадратного трехчлена: 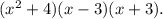
Воспользуемся методом группирования (группировки):
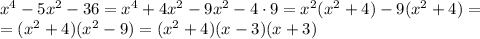
ответ: 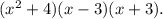
Решение на фото.
Объяснение:
Комментарий ко 2-му примеру: корни уравнения - точки пересечения графика параболы с осью OX. Если таких точек нет - график не пересекает эту ось, а значит всегда находится сверху (учитывая, что ветви параболы направлены вверх в данном случае).
Комментарий к 3-му примеру: Разделим выражение на -1, получим:
x²-10x+25 = 0. Слева - формула сокращённого умножения, а именно - квадрат разности. Он сворачивается до выражения " (x-5)² = 0 ". Если выражение в квадрате равно нулю, то и простое выражение тоже равно нулю, значит:
x - 5 = 0, откуда x = 5.

x⁴ - 5x² - 36 | x² = y
y² - 5y - 36 = 0 D = b²-4ac = 25+144 = 169
y₁₂ = (-b±√D)/2a
y₁ = (5+13):2 = 9
y₂ = (5-13):2 = -4
y² - 5y - 36 = (y - 9)(y + 4)
x⁴ - 5x² - 36 = (x² - 9)(x² + 4) = (x - 3)(x + 3)(x² + 4)