Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)
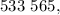 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).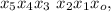


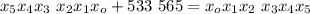 ;
;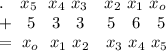

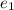 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого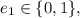
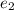 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго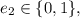
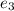 – возможная добавочная единица,
– возможная добавочная единица,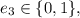
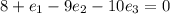 ;
;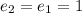 и при
и при  ;
;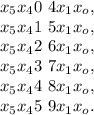
 поскольку
поскольку 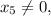 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.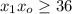 .
.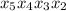 .
.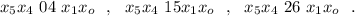
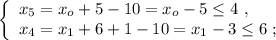

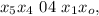
 может играть роль апреля.
может играть роль апреля.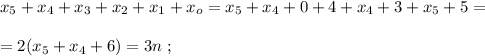
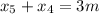 ;
;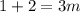 ;
;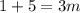 ;
;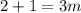 ;
; ;
;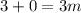 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.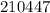 – дата 21/04/47 г.
– дата 21/04/47 г.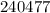 – дата 24/04/77 г.
– дата 24/04/77 г.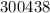 – дата 24/04/38 г.
– дата 24/04/38 г.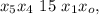
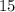 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;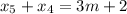 ;
;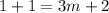 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

Объяснение:
Что тебе решить? Тут ничего нет