Объяснение:
Исходя из уравнения окружности ее центр в точке (-1;2).
Подставляем в уравнение прямой. 2 = -5 + b => b = 7
Получаем функцию y = 5x + 7
Составим систему уравнений. Далее все на фото
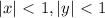
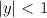возвести в квадрат, получив, 
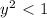, что и требовалось проверить.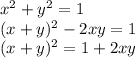
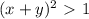
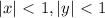, следует, что 0 <x < 1, 0 < y < 1
Объяснение:
Если кривые пересекаются, то их абциссы и ординаты в этой точек равны.
Приравняем ординаты.
(x+1)^2+(5x+b-2)^2=26
Далее решаем уравнение. В начале раскрываем оба квадрата, и все приводим к квадратному уравнению.
26*x^2+x*(10*b-18)+(b^2-4*b-21)=0
решаем его относительно x (решение прицепил как файл).
Так как точка в третьей четверти, нужен только корень с минусом (первый).