7^4
7,8^7
27^2
Для нахождения угла, найдём значения производной функции в точке касания x = -1.
y' =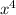 
- мы нашли производную функции.
Теперь найдём значение производной в точке касания:
y'(-1) = 1; Производная в точке касания равна 1, а значит и тангес угла наклона равен 1 (так как это и есть производная), найдём угол используя такую обратную тригонометрическую функцию как арктангенс.
tg(a) = 1 => a = arctg(1) => a = 45 градусов, где a - угол между касательной к графику функции и положительным направлением оси абсцисс.
ответ: 45 градусов.
Ну для начала возьмем все таки этот интеграл (сначал можно как неопределенный)
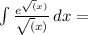{сделаем замену 
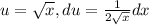} продолжаем вычисление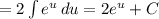 
Теперь вернемся к исходным переменным: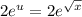 
Интеграл взяли, теперь вспоминаем формулу Ньютона-Лейбница: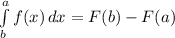 
, где F(x)-какая-либо первообразная от функции f(x). Выше мы нашли первообразную от f(x) и она оказалась равна F
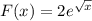, константу здесь сделали 0.
Ну и теперь получаем
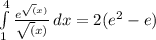
ответ: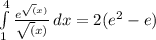
Примечание: почему я сначала брал неопределенный интеграл?
Потому что при любой замене в определенном интеграле необходимо пересчитывать пределы интегрирования.
Но поскольку мы пользуемся формулой Ньютона-Лебница в которой нам нужно найти именно первообразную, то можно воспользоваться и неопеределенным интегралом, чтобы ничего не пересчитывать.
а) 7^4
б)7.8^7
в)2/7^2
Объяснение:
^-это степень
2/7 как дробь