После начала торможения движение электропоезда описывается законом , а скорость меняется по закону v=16-0,2t, где t - время (с), v - скорость (м/с), s - пройденный путь (м). через сколько секунд поезд остановится? каков его тормозной путь? постройте графики этих функций s=s(t), v=v(t).
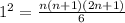
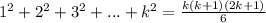
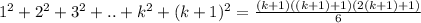
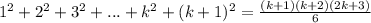
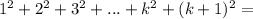
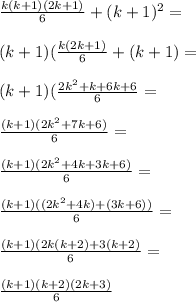
V=2t-1 то есть => v0=-1 a=2 S=v0t+at^2/2 S=-1t+2t^2/2