Для начала, можно посмотреть несколько последовательных степеней двойки: 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 Как видим, последняя цифра меняется так: 2, 4, 8, 6. А далее эта последовательность повторяется. То есть имеем повторяющуюся последовательность из четырёх цифр. Чтобы понять, на какую из этих цифр заканчивается 2^2015, мы разделим 2015 на 4. Получим 503 и остаток 3.
Чтобы далее было понятно, рассмотрим варианты: 1) если бы разделилось нацело (как, например, четвёртая степень), то число бы оканчивалось на шесть (смотри выше посчитанные степени) 2) если был бы остаток 1 (как, например, для пятой степени), то число бы оканчивалось на 2 3) если был бы остаток 2 (как, например, для шестой степени), то число бы оканчивалось на 4 4) а если остаток 3 (как, например, для седьмой степени), то число будет оканчиваться на 8
Соответственно, последняя цифра числа 2^2015 будет восемь.
А) Складываем отношения углов: 1+2+3=6 Составляем пропорцию: 6=180град. (т.к. сумма углов треугольника = 180 град.) 1=Х град. (1 здесь мера угла 1) Отсюда, Х=180 : 6 = 30 (град), т.е. угол 1 = 30 град. ответ: угол 1 = 30 градусов
Б) Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 360 град. Т.к. углы 5 + 6 = 220 град., то 360 - 220 = 140 (град) - это градусная мера внешнего угла 4 при вершине А. Отсюда, угол 1 = 180 град. - угол 4 = 180 - 140 = 40 (град.) - градусная мера угла 1 (т.к. угол 4 и угол 1 - смежные). ответ: угол 1 = 40 градусов
Следовательно,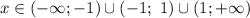
Значит, (0; 1) — единственная точка пересечения графика функции с осями координат.
Если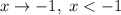 , то
, то 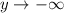 ; если
; если 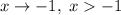 , то
, то 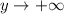 .
.
Найдем наклонные асимптоты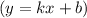 :
:
Следовательно,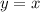 — наклонная асимптота.
— наклонная асимптота.
Найдем критические точки, приравняв первую производную к нулю: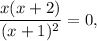 откуда
откуда 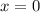 и
и  .
.
Заполним таблицу №1 (см. вложение).
Если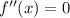 , то есть
, то есть 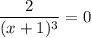 , то
, то 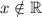 , значит, нет точек перегиба.
, значит, нет точек перегиба.
Систематизируем данные, полученные по второй производной, в таблицу №2.