♡.﹀﹀﹀﹀﹀﹀﹀﹀﹀.♡
Рассмотрите первое уравнение. Вычтите y из обеих частей уравнения.
x−y=2
Чтобы решить два уравнения методом подстановки, сначала решите одно из уравнений для одной из переменных.
x−y=2,3x−2y=9
Выберите один из уравнений и решите его для x, изолируя x в левой части знака равенства.
x−y=2
Прибавьте y к обеим частям уравнения.
x=y+2
Подставьте y+2 вместо x в другом уравнении 3x−2y=9.
3(y+2)−2y=9
Умножьте 3 на y+2.
3y+6−2y=9
Прибавьте 3y к −2y.
y+6=9
Вычтите 6 из обеих частей уравнения.
y=3
Подставьте 3 вместо y в x=y+2. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.
x=3+2
Прибавьте 2 к 3.
x=5
решение.
x=5,y=3
♡.﹀﹀﹀﹀﹀﹀﹀﹀﹀.♡
Из исходного равенства видно, что p>q, в противном случае равенство не выполнялось бы. Предположим, что p=q+k, где k - натуральное. Тогда 2q+k=(q+k-q)^3, отсюда 2q+k=k^3 или 2q=k^3-k=k(k^2-1). Тогда q=k(k^2-1)/2. Отсюда сразу видно, что q будет простым только при k=2, поскольку при k=1 получаем 0, а при k>2 будем получать составные числа, а по условию q простое. Итак, при k=2, q=2*(2^2-1)/2=3. Тогда p=q+k=3+2=5. Это единственное решение удовлетворяющее данному равенству.
ответ: p=5, q=3.
ОДЗ: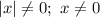
Решим данное неравенство графически.
Рассмотрим две функци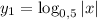и
и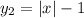 
и изобразим их на координатной плоскости (см. вложение).
Из графика видно, что логарифмическая функция не меньше модульной на промежутке![x \in [-1; \ 0) \cup (0; \ 1]](/tpl/images/1060/8330/db19d.png)
ответ:![x \in [-1; \ 0) \cup (0; \ 1]](/tpl/images/1060/8330/db19d.png)