1 задание.) Площадь прямоугольника равна произведению двух его различных сторон, а так как в прямоугольнике высотой к противоположной стороне является его сторона, то площадь можно записать как произведение стороны на высоту, проведенную к ней (эта формула свойственна для всех четырёхугольников имеющих свойства параллелограмма).
Теперь, после вступительной части, приступим к доказательству того, что площадь уменьшится.
S = a*h;
В нашем случае a1 = 1,5a, а h1 = 0,5h.
S = 1,5a*0,5h = 0,75ah; Анализируя получившиеся значение площади, можно сделать вывод, что площадь прямоугольника при данных значениях высоты и стороны составляет 75% от первоначальной площади, а это значит, что площадь прямоугольника уменьшится.
ответ: площадь уменьшится.
2 задание.)
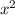+ 2x + c = 0
Решим данное квадратное уравнение и получим дискриминант, равный - (1 - с), как известно, если квадратное уравнение не имеет решений, то его дискриминант меньше нуля, в соответствии с этим утверждением решим неравенство:
1 - с < 0 => c > 1
Ближайшее значение "с" при котором уравнение не имеет решений, это 2
ответ: 2
Сначала разделим левую и правую часть уравнения на x, получим:
Решим сначала однородное уравнение, вида:
Это уравнение с разделяющимися переменными, получаем: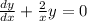
Берем интеграл от обоих частей получаем:
Дальше методом вариации свободной постоянной ищем частное решение неоднородного уравнения:
Представляем C как функцию от х, т.е C=C(x) и подставляем выражение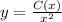
в исходное уравнение. Получаем:
Сокращаем подобные и прочее, получаем:
Подставляем получившееся значение C(x) в выражение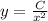
и получаем частное решение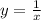 
В итоге общее решение неоднородного уравнения это сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Т.е.
Все, уравнение решено. Теперь решаем задачу Коши:
Т.к.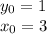
то приходим к уравнению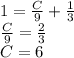
Все, нашли С, теперь пишем решение задачи Коши:
ответ: Общее решение дифференциального уравнения:
Частное решение дифференциального уравнения, удовлетворяющиего начальному условию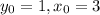
: