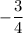Я ответила только на 5 вопросов, нонадеюсь, это Итак,
1. Да, может. Пример 19*3=57
2.С=8. Я это выявила методом подстановки.
3. Да, можно. Все плюсы и один минус в квадрате 5х5. Этот минус будет по середине. Всего в квадрате 5х5 9 квадратов 3х3. Когда нарисуешь-увидишминут если минус будет стоять по середине то он будет входить во все это. 9 квадратов.
4. 3367. Опять же методом подстановки. Умножала каждое число на 33.
5. 73. Из 73 вычла 36 получила 37.
7. Нет, получить нельзя. Если число четное, то и кончаться в квадрате оно будет на четное число=> это четное число 4. А потом перебор. Ну я по крайней мере сидела с калькулятором и перебирала квадратные корни. Из того, что я перебирала, целого квадратного корня нету.
Я ответила только на 5 вопросов, нонадеюсь, это Итак,
1. Да, может. Пример 19*3=57
2.С=8. Я это выявила методом подстановки.
3. Да, можно. Все плюсы и один минус в квадрате 5х5. Этот минус будет по середине. Всего в квадрате 5х5 9 квадратов 3х3. Когда нарисуешь-увидишминут если минус будет стоять по середине то он будет входить во все это. 9 квадратов.
4. 3367. Опять же методом подстановки. Умножала каждое число на 33.
5. 73. Из 73 вычла 36 получила 37.
7. Нет, получить нельзя. Если число четное, то и кончаться в квадрате оно будет на четное число=> это четное число 4. А потом перебор. Ну я по крайней мере сидела с калькулятором и перебирала квадратные корни. Из того, что я перебирала, целого квадратного корня нету.
Здесь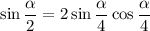 , поэтому воспользуемся основным тригонометрическим тождеством:
, поэтому воспользуемся основным тригонометрическим тождеством: 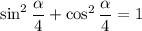
Получили систему из двух уравнений:
Сделаем замену: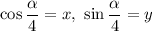
Имеем:
Получили два решения системы:
Следовательно,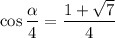 или
или 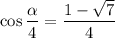 и соответственно
и соответственно 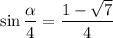 или
или 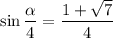
Так как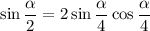 , то достаточно выбрать только одно решение, системы.
, то достаточно выбрать только одно решение, системы.
Тогда имеем:
ответ: