Выражение: x -0.8 - 2.3 - x +1.4 решите уравнения: а) -3 * (x-2.1) = 0 б) (x - 1.8 ) * (x + 5) = 0 - id10635520220131 от DimaLeonov2000 31.01.2022 01:58

Question

Алгебра: Выражение: x -0.8 - 2.3 - x +1.4 решите уравнения: а) -3 * (x-2.1) = 0 б) (x - 1.8 ) * (x + 5) = 0

DimaLeonov2000 · Accepted Answer

Задание. Прогулочный катер вышел из пункта A вниз по течению реки, которая впадает в озеро, дошёл до середины озера и отправился обратно. Найдите длину всего пути (в км), если вся прогулка заняла 3 часа, собственная скорость катера равна 24км/ч, скорость течения реки - 6км/ч, и на озере катер находился 20 минут.
Решение:
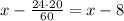Пусть длина всего пути равен х км, а путь по реке - $x- \frac{24\cdot20}{60} =x-8$ км. Скорость по течению равна (24+6=30)км/ч, а против течения - (24-6=18) км/ч. Так как катер дошёл до середины и обратно вернулся, то на весь путь он затратил 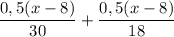$\dfrac{0,5(x-8)}{30} +\dfrac{0,5(x-8)}{18}$ что составляет 3 часа - 20 мин = 3 ч - 20/60 ч = 8/3.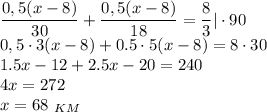

Составим уравнение

$\dfrac{0,5(x-8)}{30} +\dfrac{0,5(x-8)}{18} = \dfrac{8}{3} |\cdot 90\\ 0,5\cdot 3(x-8)+0.5\cdot 5(x-8)=8\cdot30\\ 1.5x-12+2.5x-20=240\\ 4x=272\\ x=68\,\, _{KM}$

ответ: 68 км.

Выражение: x -0.8 - 2.3 - x +1.4 решите уравнения: а) -3 * (x-2.1) = 0 б) (x - 1.8 ) * (x + 5) = 0

MOGZ ответил