Question

Вообще ничего не понимаю, заранее

Answer 1

№1.

$(5+3x^3)(25+9x^6-15x^3)$

выражение необходимо упростить по формуле суммы кубов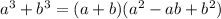 $a^3+b^3=(a+b)(a^2-ab+b^2)$

но перед этим изменим порядок одночленов в выражении, чтобы формулу можно было "собрать":

$(5+3x^3)(25+9x^6-15x^3)=(5+3x^3)(25-15x^3+9x^6)$

упрощаем:

$(5+3x^3)(25-15x^3+9x^6)=5^3+(3x^3)^3=125+27x^9$

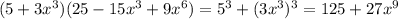
ответ: 125+27х⁹№2.$x^9+0,216y^9$

здесь применяем эту же формулу, что и в предыдущем задании, только теперь нам нужно сделать всё наоборот, т.е. "разобрать" выражение.

$\sqrt[3]{x^9} =x^3\\\sqrt[3]{0,216y^9} =0,6y^3$

$x^9+0,216y^9=(x^3+0,6y^3)(x^6-0,6x^3y^3+0,36y^6)$

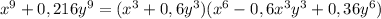
ответ: (х³+0,6у³)(х⁶-0,6х³у³+0,36у⁶)