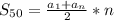- сумма арифметической пр.
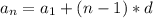- формула n-ого члена
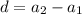- разность
Имеем:f(x)=2x^4-x+1; f'(x)=(2x^4-x+1)'=8x^3-1
Из уравнения f'(x)=0, или 8x^3-1=0, находим стационарные точки функции f(x):
8x^3=1
x^3=1/8
x=1/2=0.5
В данном случае одна стационарная точка.
В интервал [-1, 1] попадает эта точка 1/2. В ней функция принимает значение f(1/2)=f(0.5)=2*(0.5)^4-0.5+1=5/8=0.625.
В крайних точках интервала [-1,1] имеем: f(-1) = 2*(-1)^4-(-1)+1=4; f(1)=2*1^4-1+1=2.
Из трех значений f(1/2)=f(0.5)=0.625, f(-1) =4, f(1) =2 наименьшим является 0.625, а наибольшим 4.
Поэтому минимальное значение функции f(x)=2x^4-x+1в интервале [-1,1] равно 0.625, максимальное 4.
Для начала давайте вспомним, какие функции четные, какие нечетные, а какие ни четные, ни нечетные.
Если f(-x) = -f(x), то функция нечетная.
Если f(-x) = f(x), то функция четная.
Если же вышеперечисленные критерии не соблюдаются, то функция ни четная ни нечетная (функция общего вида).
Что же, тогда приступим.
____________________
Найдем F(-x):
F(-x) = - x³ + 4ctgx
F(-x) = - (x³ - 4ctgx)
Т.е, выполняется условие нечетной функции. f(-x) = -f(x) НЕЧЕТНАЯ
____________________
Найдем F(-x):
Не соблюдается ни одно из наших критериев. Следовательно наша функция НИ ЧЕТНАЯ НИ НЕЧЕТНАЯ.