Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
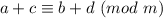
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
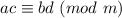
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
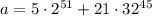
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,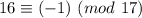 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что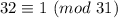 
, получаем
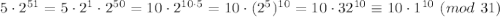
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
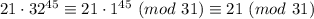
Остаток 21, чудесно. Выполняем последний шаг.
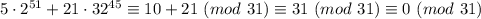
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Квадратный корень из 81 естественно равен 9: √81=9;
Далее разберемся с первым числом, имеем:
Знаменатель в степени числа всегда показывает какой у нас корень, в данном случае - корень квадратный, а квадратный корень, как известно записывается так:
Следовательно, у нас идет квадратный корень из девяти в кубе:
Квадратный корень из 729 извлекается, это 27.
Теперь второе число:
В знаменателе степени стоит 3, то есть, корень кубический. Выглядит так:
То бишь, если квадратный корень из 729 равен 27, то теперь из 27 находим квадратный корень, чтобы найти кубический корень из 729. Получаем 9.
В итоге, складывая:
27+9+9=45.