Первая встреча Гринева и Пугачева («Капитанская дочка») происходит в момент поездки Петра в Оренбург на службу. В тот день за окном стоял сильный буран, из-за которого Гринев и его слуга теряют путь и не знают, куда ехать дальше. Пугачев на тот период является еще неизвестным человеком и представляется «вожатым». Он встречается с Петром и показывает верную дорогу. Чтобы как-то отблагодарить человека, Гринев дарит ему свой теплый красивый тулуп.
Вторая встреча двух героев происходит в Белогорской крепости в момент, когда Гринев проходит службу. Пугачевские воины осаждают крепость. В тот момент Петр узнает в Пугачеве того самого «вожатого», которому он когда-то подарил тулуп за указанный верный путь. Гриневу поступает предложение перейти на сторону Пугачева, но тот отказывается, так как является верным и преданным присяге императрице. Уважая такой смелый жест, мужественность и высокоморальность, Петру дается возможность уехать из крепости целым и невредимым.
Третья встреча героев – в Оренбурге. Петр Гринев едет в крепость, чтобы возлюбленную девушку, а Пугачев ему в освобождении Маши от Швабрина. Молодые уезжают из Белогорской крепости.
Последняя встреча персонажей происходит во время Пугачевской казни на плацу, когда герои произведения встречаются взглядами. Гринев кивает головой в сторону Пугачева, они в течение минуты смотрят друг на друга, а затем происходит казнь.
Задание 4.
В задании явно видна развернутая формула суммы кубов, которую, для удобства, можно свернуть
Сумма кубов - 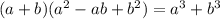
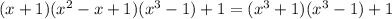
Теперь просто раскрываем скобки (можно воспользоваться формулой 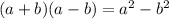 , но при этом надо знать что x будет в степени 3 · 2; чтобы не усложнять решение и не запутывать его, раскрою скобки не по формуле)
, но при этом надо знать что x будет в степени 3 · 2; чтобы не усложнять решение и не запутывать его, раскрою скобки не по формуле)
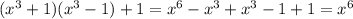
ответ: 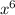 .
.
Задание 5.
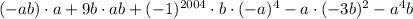
Если степень чётная, то числа в этой скобке при раскрытии, даже со знаком минус, становятся положительным и в степени, стоявшей после скобки.
Таким образом, (-ab) будет иметь нечётную (первую) степень и раскроется как -ab;
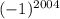 будет иметь четную степень и раскроется как 1 (при умножении 1 на любое кол-во раз получается 1);
будет иметь четную степень и раскроется как 1 (при умножении 1 на любое кол-во раз получается 1);
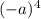 будет иметь четную степень и раскроется как
будет иметь четную степень и раскроется как 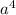 ;
;
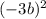 раскроется как
раскроется как 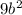 (мы умножаем каждую букву и число в скобке)
(мы умножаем каждую букву и число в скобке)
Получаем
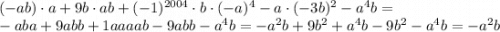
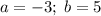
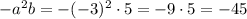
ответ: -45.
1)f(x)=2корх, х0 = 3
f(x0) = 2кор3
f'(x) = 1/(корх)
f'(x0) = 1/(кор3)
Тогда уравнение касательной:
у = 2кор3 + (1/кор3)(х - 3) = х/(кор3) + кор3.
ответ: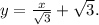
2) f(x)=18/(корх), х0=3
f(x0) = 18/кор3
f'(x) = -9/(хкорх)
f'(x0) = -3/кор3
Тогда уравнение касательной:
у = 18/кор3 - (3/кор3)(х - 3) = -хкор3 + 9кор3
ответ: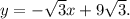
3)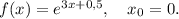
Тогда уравнение касательной:
4)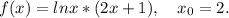
Уравнение касательной: