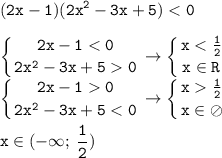
(2х-1)(2х²-3х+5)<0
отрицательное число получается тогда как перемножаются положительное и отрицательное число
2х-1>0 D=3²-4×2×5=-31 ⇒ корней нет
2x>1 а учитывая а=2>0 ⇒ 2х²-3х+5>0
x ∈(0.5;∞)
значит рассматриваем второй вариант
2х²-3х+5>0 2x-1<0
как мы уже выяснили 2x<1
x∈(-∞;∞) x∈(-∞;0.5)
(-∞;∞) ∩ (-∞;0.5) = (-∞;0.5)
ответ: х ∈ (-∞;0.5)
tgx=ctgx
tgx=1/tgx
tg^2(x)=1 =>tgx=1=> x=arctg 1+Пn,n принадлежит => x= п/4+пn,n принадлежит Z
S={п/4+пn|n принадлежит Z}
3cos2x+sin^2(x)+5sinxcosx=0
3cos2x+sin^2(x)+5sinxcosx=0
3(2cos^2(x)-1)+sin^2(x)+5sinxcosx=0
6cos^2(x)-3sin^2(x)-3cos^2(x)+sin^2(x)+5sinxcosx=0|:cos^2(x) неравный 0
6-3tg^2(x)-3+tg^2(x)+5tgx=0
Пусть t=tgx,тогда
2t^2-5t-3=0
D=25-4*2*(-3)=25+24=49
t=(5-7)/4 t=-1/2 tgx=-1/2 x=-arctg1/2+Пn,n принадлежит Z
или или или или
t=(5+7)/4 t=3 tgx=3 x=arctg3+Пk,k принадлежит Z