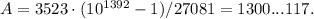
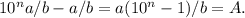Т.е. нам надо найти минимальное n, такое что 
делится на b. Такое n называется порядком числа 10 по модулю b. Т.к. b=27081=27*17*59, то достаточно найти порядки числа 10 по модулям 27, 17, 59. Они равны 3, 16, 58 соответственно. Поэтому длина периода равна НОК(3,16,58)=1392, а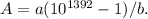 
Для того, чтобы определить, где у функции максимум, минимум, где она начинает убывать или возрастать, надо найти точки, в которых производная меняет знак. В таких точках производная либо равна 0, либо не существует.
Далее рассматриваем знак производной на промежутках:
1) (∞; -2):
y'<0 - значит на этом промежутке функция убывает
2) (-2;0):
y'>0 - функция возрастает
3) (0;2):
y'<0 - функция убывает
4) (2;+∞)
y'>0 - функция возрастает
⇒ (∞; -2) ∨ (0;2) функция ↓
(-2;0) ∨ (2;+∞) функция ↑
2. Теперь видно, что в точках с абсциссами (-2) и 2 будут минимумы, в точке с абсциссой 0 - максимум - это и есть экстремумы функции