1)
(1-2х)/(2х+1)+(х²+3х)/((2х-1)*(2х+1))+(3+х)/(2(2х+1))=
(-2*(4х²-4х+1)+2х²+6х+6х-3+2х²-х)/(2*(4х²-1))=
(-8х²+8х-2+4х²+12х-х-3)/(2*(4х²-1))=(-4х²+19х-5)/(2*(4х²-1))
Вместо плюса, скорее всего, где-то минус, может опечатка, но ответ верный.
2)
1)((6а+1)*(а+3)+(6а-1)*(а-3))/((а+3)*(а-3))=
(6а²+18а+а+3+6а²-18а-а+3)/((а+3)*(а-3))=6(2а²+1)/((а+3)*(а-3));
2) (а²-9)*6*(2а²+1)/(а²-9)*(2а²+1)=6
3)
1)((а-b)*b/(a*(a-c)))*((a-c)*(a+c)/((a-b)(a+b))=((а-b)*b(a-c)*(a+c)/((a*(a-c))(a-b)(a+b))=(ab+bc)/(a*(a+b))
(b-c)/(a+b)-(ab+bc)/(a*(a+b))=(ab-ac-ab-bc)/(a*(a+b))=-c*(a+b)/(a*(a+b))=-c/a
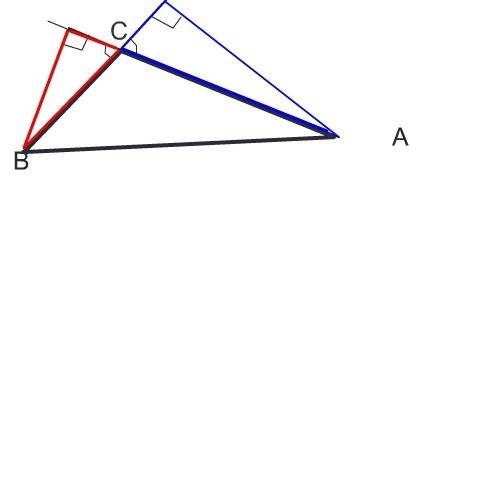
Сделайте рисунок и сразу увидите решение.
В каждом из этих треугольников один угол прямой, так как высота - это перпендикуляр, а еще по одному равны как вертикальные. Следовательно, третий угол в них тоже равен.
Эти треугольники подобны по равенству их трех углов.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
А прямоугольные треугольники подобны, если острый угол одного треугольника равен острому углу другого. Здесь острые углы - вертикальные и равны.
ответ: (а-3b)*(3a-b) Думаю что так