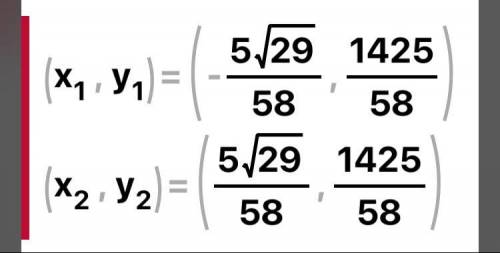
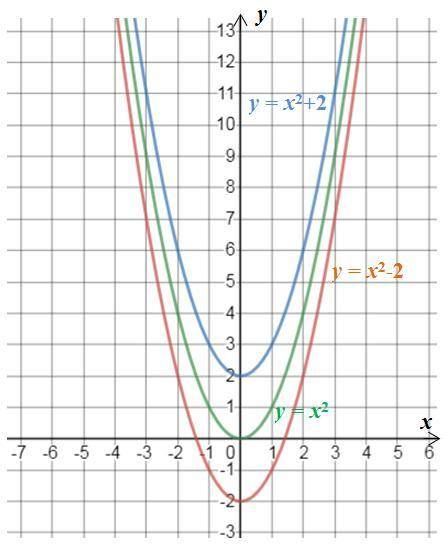
Сначала построим график функции y=x² (график этой функции – это парабола). Для этого достаточно определить 3 точки:
| x | -1 | 0 | 1 |
| y | 1 | 0 | 1 |
Для построения графиков функций y=x²-2 и y=x²+2 воспользуемся свойством (см. рисунок):
График y=f(x)+a получается из графика функции y=f(x) параллельным переносом последнего вдоль оси ординат на a единиц вверх, если a>0, и на |a| единиц вниз, если a<0.
а) Область определения функции y=x²-2: D(y)=(-∞; +∞),
Множество значений функции y=x²-2: E(y)=[-2; +∞).
b) Область определения функции y=x²+2: D(y)=(-∞; +∞),
Множество значений функции y=x²+2: E(y)=[2; +∞).
Если точка принадлежит прямой, то ее координаты удовлетворяют уравнению
1) 3x+2y= -6
М(6;2)
x=6; y=2
3*6+2*2=-6 - неверно,
N (-3;-4)
x=-3; y=-4
3*(-3)+2*(-4)=-6 - неверно,
2) 2x-3y=6
М(6;2)
x=6; y=2
2*6-3*2=6 - верно,
N (-3;-4)
x=-3; y=-4
2*(-3)-3*(-4)=6 - верно,
M и N принадлежат прямой 2x-3y=6
3) 2x+3y=-5
М(6;2)
x=6; y=2
2*6+3*2=-5 - неверно,
N (-3;-4)
x=-3; y=-4
2*(-3)+3*(-4)=-5 - неверно,
4) 3x-2y=5
М(6;2)
x=6; y=2
3*6-2*2=-5 - неверно,
N (-3;-4)
x=-3; y=-4
3*(-3)-2*(-4)=-5 - неверно
О т в е т. M и N принадлежат прямой 2x-3y=6
x1 = -sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*cos(atan2(im(y, re(y))/2)/1154 - i*sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*sin(atan2(im(y), re(y))/2)/1154)
x2 = sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*cos(atan2(im(y, re(y))/2)/1154 + i*sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*sin(atan2(im(y), re(y))/2)/1154)
Объяснение:
4 / 2 2 /atan2(im(y), re(y))\ 4 / 2 2 /atan2(im(y), re(y))\
\/ 1154 *\/ im (y) + re (y) *cos|| I*\/ 1154 *\/ im (y) + re (y) *sin||
\ 2 / \ 2 /
x1 = - -
1154 1154
4 / 2 2 /atan2(im(y), re(y))\ 4 / 2 2 /atan2(im(y), re(y))\
\/ 1154 *\/ im (y) + re (y) *cos|| I*\/ 1154 *\/ im (y) + re (y) *sin||
\ 2 / \ 2 /
x2 = +
1154 1154