ответ: 24 км/ч.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила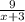 
часов и против течения реки, на расстояние в 14 км, лодки затратила 
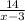часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 
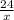часов. Составим уравнение:
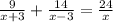
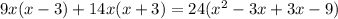
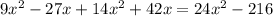
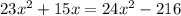
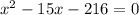
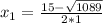
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
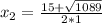
x₂=24 (км/ч) скорость лодки в стоячей воде.
ответ: 24 км/ч.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила 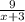часов и против течения реки, на расстояние в 14 км, лодки затратила 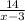часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 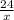часов. Составим уравнение:
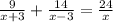
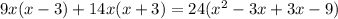
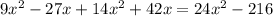
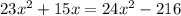
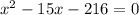
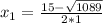
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
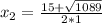
x₂=24 (км/ч) скорость лодки в стоячей воде.
Геометрическая прогрессия (bn) задана первым членом прогрессии b1 = 12 и знаменателем прогрессии q = 1/3. Для того, чтобы найти сумму бесконечно геометрической прогрессии вспомним формулу нахождения суммы бесконечно геометрической прогрессии.
S = b1/(1 - q);
где |q| < 1.
Условия, которое наложено на знаменатель геометрической прогрессии выполняется, теперь перейдем к нахождению суммы бесконечной геометрической прогрессии.
S = b1/(1 - q) =12/(1 - 1/3) = 12/(2/3) = 12 * 3/2 = 36/2 = 18.
ответ: S = 18.
Объяснение: