Задача. Двое рабочих изготавливают детали. Первый работал 5 ч., второй 8 ч. — и вместе выполнили 140 деталей. При этом первый за 2 ч. изготовит на 6 деталей меньше, чем второй за 3 ч. Сколько деталей за час выполняет каждый из них?
Решение. Пусть первый рабочий за час изготовлял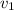 
деталей, а второй рабочий 
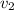деталей. Суммарный их объём работы (по формуле 
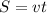, как в задачах на движение) составит 
.
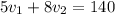Второе условие запишется так: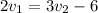 
Сложим эти два уравнения в систему:
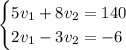
Умножим первое уравнение на 2, а второе на –5, и сложим их:
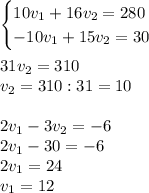
ответ: первый рабочий за час изготавливает 12 деталей, а второй — 10 деталей.
ответ:
y' = 4x^3-4x
приравниваем ее к нулю:
4x^3-4x = 0
x1 = 0
x2 = -1
x3 = 1
вычисляем значения функции
f(0) = 8
f(-1) = 7
f(1) = 7
fmin = 7, fmax = 8
используем достаточное условие экстремума функции одной переменной. найдем вторую производную:
y'' = 12x^2-4
вычисляем:
y''(0) = -4< 0 - значит точка x = 0 точка максимума функции.
y''(-1) = 8> 0 - значит точка x = -1 точка минимума функции.
y''(1) = 8> 0 - значит точка x = 1 точка минимума функции.
объяснение: