(4;  )
)
Объяснение:
Дотична може бути паралельна заданій прямій, якщо їх кутові коефіцієнти рівні між собою. Кажучи простими словами, спочатку нам потрібно знайти точку в якій похідна рівна 3 (y = 5 +3х ).
Знайдемо похідну від f(x) = x^3/3−4x^2+19x−7:
f'(х) = x^2 - 8x + 19
Прирівнюємо дане квадратне рівняння до похідної прямої ( y = 5 +3х; у' = 3):
x^2 -8x + 19 = 3
x^2-8x + 16 = 0
Згідно т.Вієта:
x1+x2 = 8
x1*x2 = 16
x1 = 4; х2 = 4
Але це тільки абсциса, щоб знайти ординати потрібно підставити знайдені точки в рівняння функції:
f(4) = 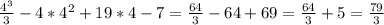
По суті, у нас два кореня рівняння x1 = 4 і x2 = 4 і ми повинні були записати дві точки, однак оскільки у нас відбулося співпадіння точок, то у відповідь можна записати одну, тобто (4;  )
)
Находим точки, в которых неравенство равно нулю:
x-1=0 x=1
x+5=0 x=-5
Наносим на прямую (-∞;+∞) эти точки:
-∞-51+∞
Получаем три диапазона: (-∞;-5) (-5;1) (1;+∞)
Для того, чтобы определить знак диапазона достаточно подставить хотя бы одно число из этого диапазона:
(-∞;-5) Например, подставим число -7: (-7-1)(-7+5)=-8*(-2)=16>0 ⇒ +
(-5;1) Подставим число этого диапазона 0: (0-1)(0+5)=-1*5=-5<0 ⇒ -
(1;+∞) Подставим 2: (2-1)(2+5)=1*7=7>0 ⇒ +
-∞+-5-1++∞ ⇒
x∈(-∞;-5)U(1;+∞).