картина и.тихого "аисты" красочная.художник когда писал эту карину наверняка использовл много яркой краски,значит у него была большая палитра цветов.картина запечетлена в том моменте когда аисты подымаются ввысь.перья у аистов белые и местами голубые.интересно было бы узнать,зачем подымаются вверх эти птицы.может ,их кто-то спугнул или они решили полетать в воздухе..остается только догадываться.облака на картине белые,нет не единого серого облачка.смотря на картину,на душе радностно.смотря на нее можно говорить многого,но это только часть того чего я могу передать на листе бумаги.
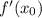производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.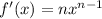
- где n это степень.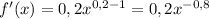
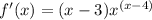
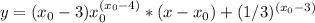
и получаешь уравнение касательной.
(4-y)²=y²-8y+16
1) (y-7)²=y²-14y+49
2) (4a+3b)²=16a²+24ab+9b²
3) (a-4)(a+4)=a²-16
4) (5m+6n)(6n-5m) =30mn-25m²+36n²-30mn=-25m²+36n²=36n²-25m²