В мешке 48 В сундуке 144
Объяснение:
Пусть x - количество монет в мешке, а значит в сундуке: 3x монет. После того, как из мешка переложили 24 монеты, в сундуке стало: 3x+24, а в мешке x−24. И если в сундуке их стало в 7 раз больше чем в мешке, то имеем: 3x+24=7(x−24).
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно x и записать ответ.
Решим полученное уравнение: 3x+24=7(x−24). Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: 3x+24=7x−7⋅24. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит x в левую, получим: 24+7⋅24=7x−3x. После упрощения получили 192=4x, разделим обе части уравнения на коэффициент при неизвестном, т.е на 4, тогда получим x=48.
За переменную x мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.е 3x.
Монет в мешке: 48
Монет в сундуке: 48⋅3=144
Объяснение:
1) при х≥3
y=4|x-3|-xˆ2+8x-15=4(x-3)-xˆ2+8x-15=4x-12-xˆ2+8x-15=-х^2+12x-27
координаты вершины 12/2=6; y(6)=-36+72-27 (6;9)
пересечение с осью ОХ -х^2+12x-27=0 х^2-12x+27=0
х₁-₂=(12±√144-108)/2=(12±6)/2={3;9}
2) при х<3
y=4|x-3|-xˆ2+8x-15=-4(x-3)-xˆ2+8x-15=-4x+12-xˆ2+8x-15=-х^2+4x-3
координаты вершины 4/2=2; y(2)=-4+8-3=1 (2;1)
пересечение с осью ОХ х^2+4x-3=0 х^2-4x+3=0
х₁-₂=(4±√16-12)/2=(4±2)/2={1;3}
в точке 3 два графика пересекаются
3) построение
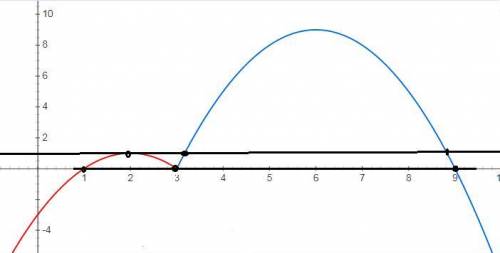
при x<3 строим график у=-х^2+4x-3
при х≥3 строим график у=-х^2+12x-27
по вершинам и точкам пересечения с осью ОХ
4) y=m имеет с графиком ровно три общие точки при
m=0
m= 2 (вершина графика у=-х^2+4x-3)
Объяснение:
Проверка: