Объяснение:
(х+4)(х+3)(х+2)(х+1)-120=0 ;
групуємо множники так :
[(х+4)(х+1)] [(х+3)(х+2)] - 120 = 0 ;
( x² + 5x + 4 )( x² + 5x + 6 ) - 120 = 0 ;
позначимо x² + 5x + 4 = у , тоді
у * ( у + 2 ) - 120 = 0 ;
y² + 2y - 120 = 0 ; D = 484 > 0 ; y₁ = - 12 ; y₂ = 10 .
Маємо два простих рівняння :
x² + 5x + 4 = - 12 ; x² + 5x + 4 = 10 ;
x² + 5x + 16 = 0 ; x² + 5x - 6 = 0 ;
D = - 39 < 0 ; D = 49 > 0 ;
xЄ ∅ ; x₁ = - 6 ; x₂ = 1 .
В - дь : - 6 і 1 .
1. Выражение 2х²у³х³ - одночлен в стандартном виде.(-)
2. Выражение, представляющее собой сумму одночленов – многочлен.(+)
3.Одночлены с одинаковой буквенной частью – подобные одночлены. (+)
4.В выражении (5х) ³ число “3” - основание. (-)
5.Квадрат двучлена (а-2в) равен а²-4ав+4в² . (+)
6.Выражение (х²-у²) представляет собой разность квадратов. (+)
7. (х³+у³)- куб суммы. (-)
8. Уравнение х² -25=0 имеет два корня 5 и -5. (+)
9.Выражение 16х4у6 -это квадрат одночлена 8х²у³. (-)
2 вариант
1.Степень одночлена 2х²у³z³ равна 18. (-)
2. Многочлен- это выражение, представляющее собой сумму одночленов. (+)
3.В выражение *+ 14в+49 , * - это в2. (+)
4.Выражение -(-5х³) 2 равно 25х6 . (-)
5.Квадрат двучлена (9а6-2в³) равен 81а12-36а6в³+4в6 . (+)
6.Выражение (х-у) ³ представляет собой куб разности. (+)
7.Уравнение в2 +81 = 0 имеет два корня. (-)
8.Выражение (х+5) ² всегда больше или равно 0. (+)
9.Выражение 16х4у12 -это четвертая степень одночлена 4ху³. (
есть только ответы на 9 вопросов)
Объяснение:
Объяснение:
1 функция не имеет решений при x=0 и при x=-5/3
y=kx - прямая, если k=0, то пересечений с 1 графиком функции не будет, значит определим значение функций в точке x=5/3
y=0.6, определим чему равен значение коэффициента k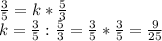
Строим прямую через точки (0;0) и (5/3; 3/5)