При любом а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии
Объяснение:
Решение в приложении
У кубической параболы будет всего один центр симметрии. В точке с абсциссой ординатой . Эта точка совпадает с точкой перегиба.
Если посмотреть скриншоты, то только в случае выполняется условие центра симметрии.
Это можно было бы доказать с параллельного переноса, растяжения и сжатия, поворота кубической параболы y=x³. Любая другая парабола получается из исходной с этих преобразований.
Интересно еще вот что, в формуле Кардано для решения кубического уравнения первая подстановка именно .
1)Все жители не могут быть лгунами, иначе каждый из них сказал бы правду(противоречит условию).
2)Возьмем случайного рыцаря. Из утверждения вытекает, что лжецов на острове больше, чем (2015−1)\2=1007, то есть не менее 1007 лжецов.
3)Возьмем случайного лжеца. Его заявление ложно,т.к. кроме него не более половины жителей острова — лжецы. получается, что кроме него на острове не более 2014\2=1007 лжецов (то есть не более 1007), т.е. вместе с ним лжецов не более 1007.
4)из 2) и 3) следует, что: единственный вариант - это когда на острове ровно 1007 лжецов.
При любом а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии
Объяснение:
Решение в приложении
У кубической параболы будет всего один центр симметрии. В точке с абсциссой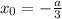
ординатой 
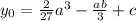. Эта точка совпадает с точкой перегиба.
Если посмотреть скриншоты, то только в случае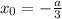
выполняется условие центра симметрии.
Это можно было бы доказать с параллельного переноса, растяжения и сжатия, поворота кубической параболы y=x³. Любая другая парабола получается из исходной с этих преобразований.
Интересно еще вот что, в формуле Кардано для решения кубического уравнения первая подстановка именно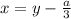
.