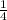
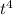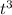−
+2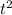
где S измеряется в метрах, t - в секундах. В какой момент времени ускорение равняется 1?
2*4^x-3*10^x=5*25^x
Разделим правую и левую части на 25^x. Получим
4^x 10^x
2 - 3 = 5
25^x 25^x
Так как степени у числетелей и знаменателей одинаковые можно поступить следующим образом
2* (4 : 25)^х - 3*(10 : 25)^х = 5
Во второй дроби можно сократить 10 и 25 на 5. Получаем
2* (4 : 25)^х - 3*(2 : 5)^х = 5
Так как 4 = 2^2, a 25 = 5^2, получим следующее
2* (2 : 5)^2х - 3*(2 : 5)^х = 5
Введем новую переменную t = (2 : 5)^х
Получим новое уравнение
2*t^2 - 3*t = 5
2*t^2 - 3*t - 5 = 0
Решаем через дискриминант. a = 2, b = -3, c = -5
D = b^2 -4ac = 9 - 4*2*(-5) = 9 + 40 = 49
t(1) = (3 - 7) : 4 = -1
t(2) = (3 + 7) : 4 = 2,5
x = -1 нам не подходит, так как ни при каких х (2 : 5)^х не будет отрицательным.
Тогда получаем
(2 : 5)^х = t(2)
(2 : 5)^х = 5 : 2
(2 : 5)^х = (2 : 5)^(-1)
х = -1
49х = 4у + 9
35х = 3у + 5
3у=35х-5
3у=5(7х-1)
у=5(7х-1)/3
49х = 4*5(7х-1)/3 + 9
49х=140х-20+27/3
49х*3=140х+7
147х-140х=7
7х=7
х=1
у=5(7*1-1)/3
у=5*6/3
у=5*2
у=105х - 4у = 5 | *(-5)
-25х + 20у = -25
а теперь складываем строки системы уравнений
25х - 18 у = 75
-25х + 20у = -25
0х +2у = 50
т. е. 2у = 50
у = 25
для того чтобы найти х, подставляем полученное значение у в любое уравнение
5х -4*25 = 5
5х - 100 = 5
5х = 5 + 100
5х = 105
х= 105/5
х = 21
ответ
х=21
у=25.
-3u+5v=1.5 домножим обе части уравнения на -3,получаем
9u-15v=4.5
система принимает вид. можем применить метод сложения (аналогично А)
11u+15v=1.9
9u-15v=4.5
2х-3у = -8
х=7-4у2(7-4у) -3у = -8
х=7-4у
14-8у-3у+8=0
х=7-4у
22=11у
х=7-4у
у=2
х=7-8
у=2
х=-1
20v=6.4
v=0.32