Для начала разберемся с ОДЗ:
x + 6 > 0 ⇒ x > - 6
х + 6 ≠ 1 ⇒ х ⇒ - 5
x / (x-4) > 0
+ 0 - 4 +
_______⚪_________⚪_______
/////////////// ////////////////
x ∈ ( - ∞ ; 0 ) ∪ ( 4 ; + ∞)
Приступим:
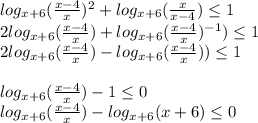
Дальше Необходимо вспомнить одну из формул рационализации:
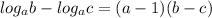
Тогда:
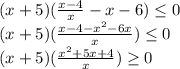
Приравняем к 0 и решим квадратное уравнение, дабы разложить эту часть на множители.
x² + 5x + 4 = 0
D = b² - 4ac = 9
x(1) = (-b-√D)/2a = - 4
x(2) = (-b+√D)/2a = - 1
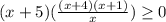
Воспользуемся методом интервалов:
+ -5 - -4 + -1 - 0 +
_____⚫______⚫______⚫______⚪_____________
////////// ////////////// /////////////////////
x ∈ ( - ∞ ; - 5] ∪ [ - 4 ; - 1 ] ∪ ( 0 ; + ∞)
Подставим под ОДЗ и получим ответ:
ответ: ( - 6 ; - 5] ∪ [ - 4 ; - 1 ] ∪ ( 4 ; + ∞)
Объяснение:
3x^2 -2x=0; D=4-0=4
x1=(2-2)/6=0
x2=(2+2)/6=2/3
ответ: 0 и 2/3.
2x^2 +3x=x^2
2x^2 +3x-x^2=0
x^2 +3x=0; D=9-0=9
x1=(-3-3)/2=-6/2=-3
x2=(-3+3)/2=0
ответ: -3 и 0.
2x^2 -18=0 |2
x^2 -9=0; D=0+36=36
x1=-6/2=-3
x2=6/2=3
ответ: -3 и 3.
4x=9
Через дискриминант это уравнение не будет решаться, так как при определении корня знаменатель будет равняться 0, что недопустимо:
4x-9=0; D=16+0=16
x=(-4-4)/(2•0)=пустое множество.
Без дискриминанта:
4x=9; x=9/4=2 1/4=2,25
ответ: 2,25.
А если:
4x^2=9
4x^2 -9=0; D=0+144=144
x1=-12/8=-3/2=-1,5
x2=12/8=1,5
ответ: -1,5 и 1,5.
3x^2 -9=0 |3
x^2 -3=0; D=0+12=12
x1=(-√12)/2=-√(12/4)=-√3
x2=(√12)/2=√3
ответ: -√3 и √3.
5x^2 +1=0; D=0-20=-20
При D<0 уравнение не имеет решений.