Question

Высоту над землей подброшенного вверх мяча вычисляют по формуле
h(t)=12t-5t"2, h- высота в м, t - время в секундах.
А. На какой высоте будет мяч через три секунды?
Б. Через сколько секунд мяч будет находиться на высоте 7м?
В. Какой наибольше высоты достиг мяч

Answer 1

А).

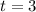Через $t=3$ секунды мяч будет на следующей высоте:

$h(3)=12 \cdot 3 - 5 \cdot 3^2 = 36-45=-9$

Б).

Здесь нужно найти такое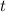 $t$, при котором выполняется $h(t)=7$.

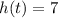Составим уравнение и решим его:

$12t-5t^2=7\\\\5t^2-12t+7=0\\\\x_1=\dfrac{-(-12)+\sqrt{(-12)^2-4 \cdot 5 \cdot 7} }{2 \cdot 5} = 1,4\\\\x_2 = \dfrac{-(-12)-\sqrt{(-12)^2-4 \cdot 5 \cdot 7} }{2 \cdot 5} = 1$

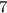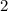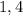Следовательно, мяч побывает на высоте $7$ метров ровно $2$ раза: через $1$ и через $1,4$ секунды после своего отправления.

В).

Раз коэффициент при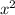 $x^2$ отрицательный (он равен 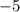$-5$), то ветви параболы направлены вниз и максимальное значение функции 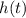$h(t)$ будет достигаться в вершине параболы, которая имеет абсциссу 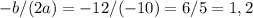$-b/(2a) = -12/(-10) = 6/5=1,2$. Теперь найдем само 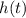$h(t)$ в этой точке (ординату):

$h(1,2) = 12 \cdot 1,2 - 5 \cdot (1,2)^2 = 7,2$

Делаем вывод, что наибольшая высота, которую достиг мяч - это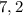 $7,2$ метра.