Question

Монета подброшена 120 раз. Найти вероятность следующих событий: а) гербов выпало ровно 60 раз; б) герб выпал не меньше 50 или больше 70 раз

Answer 1

Всего n = 120 испытаний. Вероятность успеха в одном испытании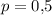 $p=0{,}5$, соответственно вероятность противоположного события $q=1-p=0{,}5$.

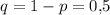а) Для больших n будем использовать локальную теорему Лапласа

$x=\dfrac{k-np}{\sqrt{npq}}=\dfrac{60-120\cdot 0{,}5}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}=0$

Искомая вероятность: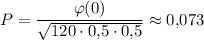 $P=\dfrac{\varphi(0)}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}\approx 0{,}073$

где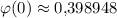 $\varphi(0)\approx 0{,}398948$.

б) Применяем форму интегральной теоремы Лапласа

$x_1=\dfrac{k_1-np}{\sqrt{npq}}=\dfrac{50-120\cdot 0{,}5}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}\approx -1{,}83;\\ \\ x_2=\dfrac{k_2-np}{\sqrt{npq}}=\dfrac{70-120\cdot 0{,}5}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}\approx 1{,}83$

Искомая вероятность:

$P_{120}\Big(50$