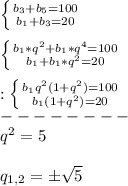
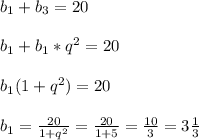
Формула объема призмы: Площадь основания (Sосн.) умножить на высоту (h), тобишь:
Vпризмы=Sосн.*h
Площадь основания правильного шестиугольника равна: три корня из трех на два умножить на сторону в квадрате(a), тобишь:
Sосн.=3√3/2*a^2
Из текста задачи ясно, что объем не изменился. Получаем: V1=V2, а сторона основания второй призмы в два раза меньше, и обозначив сторону первой за a, сторону второй обозначим через a/2.
Приравниванием формулы объема первой и второй призмы,обозначаем искомую высоту через x и получаем уравнение:
3√3/2*a^2*24=3√3/2*a^2/4*x
Делим обе части уравнения на 3√3/2 и получаем:
a^2*24=a^2/4*x
Чтобы избавится от знаменателя во второй части домнажаем обе части на 4:
96*a^2=a^2x
x=96a^2/a^2
В результате a^2 сокращается и остается 96:
x=96.
ответ:96 см.
ответ: b₁=10/3 q=±√5.
Объяснение: a₁=? q=?
{b₃+b₅=100 {b₁q²+b₁q⁴=100 {b₁q²*(1+q²)=100
{b₁+b₃=20 {b₁+b₁q²=20 {b₁*(1+q²)=20
Разделим первое уравнение на второе:
q²=5
q=±√5
b₁*(1+q²)=20
b₁=20/(1+q²)=20/(1+(±√5)²)=10/(1+5)=20/6=10/3.