14x²=7
уравниваем обе части к х²
x²=0.5
x=±√0.5
ответ: ±√0.5
№2
5x²-x=0
выносим x за скобку
x(5х-1)=0
если в произведении два выражения дают ноль то одно из выражений равно нулю ⇒ х₁=0 и 5х₂-1=0
х₂=0,2
ответ: 0 и 0,2
6+х²=0
х²=-6
х=±√-6 так как из отрицательных выражений вычленять корень квадратный невозможно, то в данном уравнении корней нет
ответ: ∅
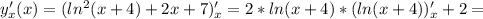
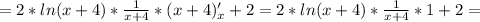
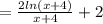
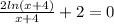
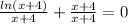
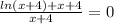
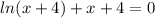
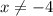для него сохраняется.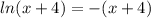
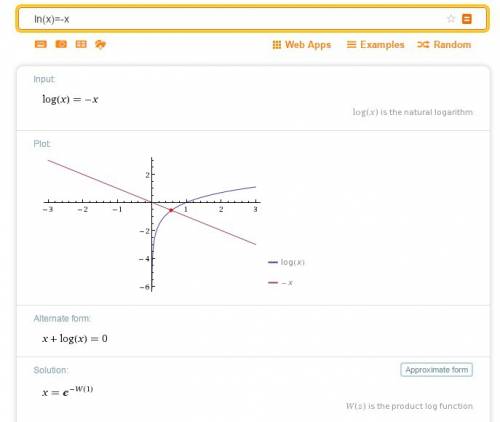
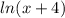монотонно растет, функция же 
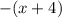монотонно убывает, что означает, что у уравнения существует лишь один корень.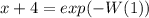
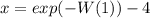
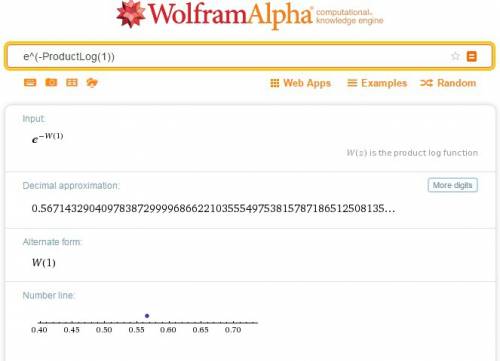
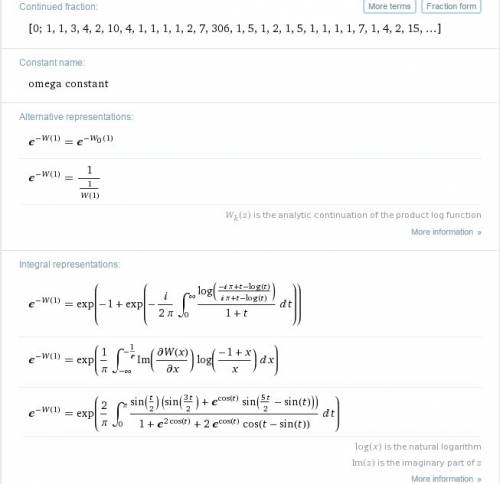
в бесконечность, действительные значения исследуемой функции также тогда устремятся в бесконечность:
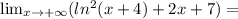
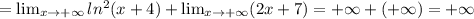
, она непрерывно растет.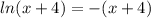
x и y - натуральные числа, значит числа y-x и y+x - целые.
y^2-x^2=123
(y-x)(y+x)=123
123 можно записать в произведение двух целіх чисел следующим образом
123=1*123=(-1)*(-123)=3*41=(-3)*(-41).
Значит получаем восемь систем уравнений
первая
y-x=1
y+x=123
y=(1+123)/2=62
x=(123-1)/2=61
(61;62) - подходит
вторая
y-x=123
y+x=1
x=(1-123)/2=-61 - не натуральное, не подходит
третья
y-x=-1
y+x=-123
не подходит так как сумма двух натуральных чисел число натуральное, а значит неотрицательное
четвертая
y-x=-123
y+x=-1
не подходит так как сумма двух натуральных чисел число натуральное, а значит неотрицательное
пятая
y-x=3
y+x=41
y=(41+3)/2=22
x=(41-3)/2=19
(19;22) - подходит
шестая
y-x=41
y+x=3
x=(3-41)/2=-19 - не подходит
седьмая
y-x=-3
y+x=-41
и восьмая
y-x=-41
y+x=-3
не подходят так как сумма двух натуральных чисел число натуральное, а значит неотрицательное
ответ: (19;22),(61;62)
Объяснение:
а) х^2=1/2
x=+-(1/2)^1/2 ^1/2-степень квадратного корня, то есть просто корень
б) 5х^2-x=0
х(5х-1)=0
х=0 и 5х-1=0
5х=1
х=1/5
в) 6+x^2=0
x^2=-6
Корней нет, так как из отрицательного числа корень не извлекается