функция y=x²+x-9?
если да, то находим вершину графика функции по формуле m=-b/2a; m=-1/2=-0,5.
(-0,5;-9,25)- вершина параболы.
функция принимает отрицательные значения, то есть y<0, при x²+x-9>0.
решим неравенство: x²+x-9>0
x²+x-9=0
D=b²-4ac;
D=1+36=37≈6.08²
x₁,₂=(-1±6.08)/2;
x₁=-3.54; x₂=2.54.
Методом интервалов расскатляем знаки и мы получаем,
что y<0, при x∈(-3,54; 2,54). Но это всё примерные значения.
Если 0<x<4.
Просто подставим в функцию x=0 и x=4.
При x=0, y=-9; при x=4, y=11.
Так как неравенство у нас строгое, значит y∈(-9;11).
НУ смотри, путь равен произведению скорости тела на время, значит, из этой формулы, время равно отношению пути к скорости тела.
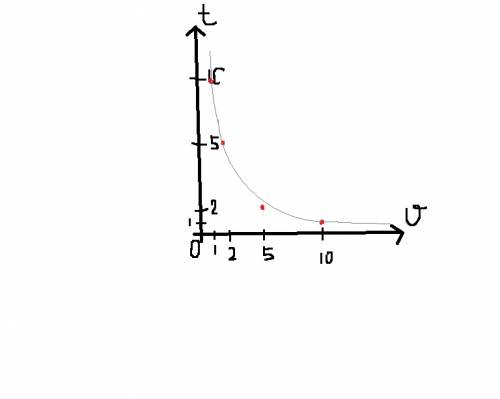
t=S/v, то есть t=10/v. У тебя получилась функция, только с другими переменными (сравни, y=10/x-обратная пропорциональность, график гипербола).
Строишь график, вместо х пишешь v, а вместо у пишешь t. Но стоишь гиперболу только в первой координатной четверти, так как время не может быть отрицательным.
ПРОСТИ ЗА ТАКОЙ РИСУНОК! Мои навыки художника никуда не годятся)))
Даны уравнения линейных функций у= -х-3 у=3х+5
Графики прямые линии.
Чтобы найти значение х точки пересечения двух данных прямых, приравняем их правые части, так как левые равны:
-х-3=3х+5
-х-3х=5+3
-4х=8
4х= -8
х= -2
Чтобы найти значение у точки пересечения двух данных прямых, найденное значение х подставляем в любое уравнение из данных:
у= -х-3 = -(-2)-3 = 2-3 = -1
у=3х+5 = 3*(-2)+5 = -6+5 = -1
Координаты точки пересечения (-2; -1)