22. -2
23. 1
Объяснение:
22. Рассмотрим каждое из подкоренных выражений:

Поскольку квадрат какого-либо числа неотрицателен, 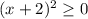 , отсюда:
, отсюда:

Значит, левая часть ![\sqrt[3]{2x^2+8x+72}+\sqrt[3]{3x^2+12x+12}\geq \sqrt[3]{64}+\sqrt[3]{0}=4](/tpl/images/4540/3998/87f22.png)
Правая часть 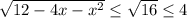
Левая часть не меньше 4, а правая не больше 4. Значит, равенство достигается тогда и только тогда, когда обе части равны 4. Правая часть равна 4:
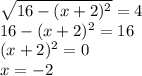
Проверим этот корень для левой части:
![\sqrt[3]{2(-2+2)^2+64}+\sqrt[3]{3(-2+2)^2}=\sqrt[3]{64}+\sqrt[3]{0}=4](/tpl/images/4540/3998/4cb78.png) — верно.
— верно.
Уравнение имеет единственный корень x = -2.
23. Заметим, что 
Значит, 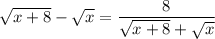 (знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит,
(знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит, 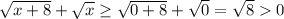 ).
).
Пусть  . Тогда уравнение имеет вид:
. Тогда уравнение имеет вид:
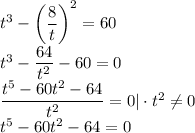
Заметим, что t = 4 — корень многочлена левой части. Поделив его столбиком на (t - 4), получим его разложение на множители:

Поскольку t > 0,  , значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:
, значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:

Левая часть неотрицательна, значит, правая часть также неотрицательна: 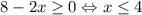
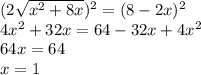
Корень удовлетворяет условиям 0 ≤ x ≤ 4, значит, он подходит.
y= -x² + 4x - 3
Объяснение:
Построить график функции, это парабола cо смещённым центром, ветви параболы направлены вниз.
а)найти координаты вершины параболы:
х₀ = -b/2a = -4/-2 = 2
y₀ = -(2)²+4*2-3 = -4+8-3 = 1
Координаты вершины (2; 1)
б)Ось симметрии = -b/2a X = -4/-2 = 2
в)найти точки пересечения параболы с осью Х, нули функции:
y= -x²+ 4x - 3
-x²+ 4x - 3=0
x²- 4x + 3=0, квадратное уравнение, ищем корни:
х₁,₂ = (4±√16-12)/2
х₁,₂ = (4±√4)/2
х₁,₂ = (4±2)/2
х₁ = 1
х₂ = 3
Координаты нулей функции (1; 0) (3; 0)
г)Найти точки пересечения графика функции с осью ОУ.
Нужно придать х значение 0: у= -0+0-3=-3
Также такой точкой является свободный член уравнения c, = -3
Координата точки пересечения (0; -3)
д)для построения графика нужно найти ещё несколько
дополнительных точек:
х=-1 у= -8 (-1; -8)
х= 0 у= -3 (0; -3)
х=4 у= -3 (4;-3)
х= 5 у= -8 (5;-8)
Координаты вершины параболы (2; 1)
Координаты точек пересечения параболы с осью Х: (1; 0) (3; 0)
Координаты дополнительных точек: (-1; -8) (0; -3) (4;-3) (5;-8)
e)В первой, третьей и четвёртой четвертях.
Объяснение:
система:
3x-3y=6
2x-3y=2 |*(-1)
система:
3х–3у=6 (ур1)
–2х+3у=—2 (Ур 2)
сложим уравнения (1) и (2), получим:
х=4
подставим значение х в уравнение (1), получим:
12–3у=6
–3у=6
у=–2
2) система:
x-2y=-2 (ур 1)
4x+2y=2 (Ур 2)
сложим уравнения (1) и (2), получим:
5х=0
х=0
подставим значение х в уравнение (1), получим:
0–2у=–2
–2у=–2
у=1
3) система:
3x+3y=9
2x+3y=8 |*(–1)
система:
3x+3y=9 (Ур 1)
–2х–3у=–8 (Ур 2)
сложим уравнения (1) и (2), получим:
х=1
подставим значение х в уравнение (1), получим:
3+3у=9
3у=6
у=2
4) система:
6x-10y=4
2x+3y=-5 |*(–3)
система:
6x-10y=4 (ур 1)
–6х–9у=15 (ур 2)
сложим уравнения (1) и (2), получим:
–19у=19
у=–1
подставим значение у в уравнение (1), получим:
6х+10=4
6х=–6
х=–1
5) система:
2x+6y=-4 |*(–1)
2x+9y=5
система:
–2х–6у=4 (ур 1)
2x+9y=5 (Ур 2)
сложим уравнения (1) и (2), получим:
3у=9
у=3
подставим значение у в уравнение (1), получим:
–2х–18=4
–2х=22
х=–11
6) система:
5x+2y=6 |*3
3x+7y=-8 |*(–5)
система:
15х+6у=18 (Ур 1)
–15х–35у=40 (Ур 2)
сложим уравнения (1) и (2), получим:
–29у=22
у=– 22/29
подставим значение у в уравнение (1), получим
15х– 132/29=18
15х=18 132/29
х=1 73/145