Вычислите при х= -1 значение многочлена х² - 6х - 7.
Упростить ничего нельзя, поэтому просто подставим вместо x -1:
(-1)² - 6 * (-1) - 7
Дальше всё просто: любое число в четной степени положительно, значит (-1)² = 1, это можно доказать: т.к. aⁿ = a * a * a n раз, значит (-1)² -- это -1 * (-1) 2 раза, отсюда -1 * (-1) = 1, поэтому (-1)² = 1.
Отрицательное число, умноженное на отрицательное число, даёт положительное число, значит: -6 * (-1) = 6. Получаем следующее:
(-1)² - 6 * (-1) - 7 = 1 + 6 - 7 = 7 - 7 = 0.
ответ: значение выражения x² - 6x - 7 при x = -1 равно 0.
© Rahmann
1)f(x)=
2)
возьмем производную
(-x^3-2x^2+4x+5)=-3x^2-4x+4
найдем нули производной т.е.дискриминант)
-3x^2-4x+4=0
D/4=4+12=16=4
x=2+4=-2
x=2-4=2/3
отложим корни
расставим знаки
функция убывает на [-2;2/3]
функция возростает на (-бесонечности;-2]u[2/3;+бесконечности)
3)f(x)=x^4-8x^3-10
так же возьмем производную
x^4-8x^3-10=4x^3-24x^2
4x^3-24x^2=0
4x^2(x-6)=0
x=0 x=6
отложим корни
расставим знаки
функция убывает на (-бесконечности;6]
функция возростает на [6;+бесконечности)
4)f(x)=(x^2+2x)/(4x-1)
производная
(x^2+2x)/(4x-1)=((2x+2)(4x-1)-4(x^2+2x))/(4x-1)^2=(4x^2-2x-2)/(4x-1)^2=((x-1)(x+1/2))/(4x-1)^2 ООФ x не равен 1/4
нули производной
x=1
x=-1/2
отложим корни
расставим знаки
функция убывает на [-1/2;1/4)u(1/4;1]
функция возростает на (-бесконечности; -1/2]u[1;+бесконечности)
Подставляем вместо x данное значение и вычисляем:
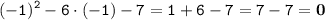
ответ: