Решение методом разложения:
Разложим числа на простые множители и подчеркнем общие множители чисел:
58110697294650 = 2 · 3 · 3 · 3 · 5 · 5 · 7 · 7 · 7 · 11 · 11 · 13 · 13 · 17 · 19 · 19
3191270940 = 2 · 2 · 3 · 3 · 3 · 5 · 11 · 11 · 13 · 13 · 17 · 17
Общие множители чисел: 2; 3; 3; 3; 5; 11; 11; 13; 13; 17
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД обоих чисел = 2 · 3 · 3 · 3 · 5 · 11 · 11 · 13 · 13 · 17 = 93860910
Решение методом Евклида:
1) 58110697294650 : 3191270940 = 18209 (ост. 844748190)
2) 3191270940 : 844748190 = 3 (ост. 657026370)
3) 844748190 : 657026370 = 1 (ост. 187721820)
4) 657026370 : 187721820 = 3 (ост. 93860910)
5) 187721820 : 93860910 = 2 без остатка.
Значит, 93860910 является НОД.
Примечание:
Проверку прикрепил фотографией.
ответ: НОД = 93860910.
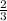от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
Координаты точки пересечения двух прямых (-6; 10)
Объяснение:
x+y-4=0 3x+2y-2=0
Преобразуем уравнения в более удобный для вычислений вид:
у=4-х 2у=2-3х у=(2-3х)/2
Уравнения линейной функции, графики - прямые линии.
Для того, чтобы ответить на вопрос задания, нужно найти координаты точки пересечения данных прямых (если она существует).
Чтобы найти абсциссу (значение х) приравняем правые части уравнений (левые равны):
4-х = (2-3х)/2, избавимся от дробного выражения, умножим обе части уравнения на 2:
8-2х=2-3х
-2х+3х=2-8
х= -6
Подставим найденное значение х в любое из двух данных уравнений, найдём значение у:
у=4 - (-6) = 4+6=10
у=(2-3*(-6))/2 у=(2+18)/2 у=10
Координаты точки пересечения двух прямых (-6; 10)
Вывод: точка пересечения не лежит на координатных осях.
Если бы она лежала на оси У, то х был бы равен 0,
а если бы на оси Х, то у был бы равен 0.