


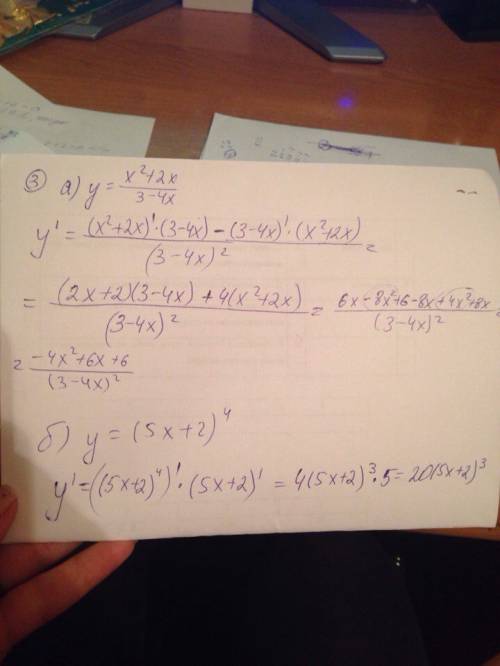
1. Выпадение 2 очков при 1 бросании = 6, при втором бросании, тоже = 6, значит равновозможных исходов 6*6=36
2. Для того, чтобы 2 очка были наименьшими из выпавших, при первом броске должно выпасть 2, при втором броске - любое количество очков, кроме 1. Или при первом броске - любое, кроме 1, а при втором броске - 2 очка.
3. Возможен вариант выпадения 2 очков и при 1 и при 2 броске, поэтому, при подсчете, вариант это учитывается 2 раза.
3. Выпадение 2 очков из всех, кроме 1 очка = 5, при первом, и 5 при втором броске:
количество благоприятных исходов: 5+5-1=9 ((-1) - выпадение 2 очков в каждом из двух бросаний)
4. Вероятность благоприятного исхода: 9/36=1/4=0.25
ответ: 0.25
x=(-1±√17)/2
Объяснение:
ОДЗ: x²+x≥0; x²+x+5≥0; 2x²+2x+17≥0⇒x∈(-∞;-1]∪[0;+∞)
(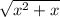 +
+ 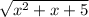 )²=(
)²=(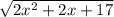 )²
)²
2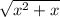
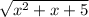 =12
=12
(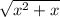
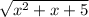 )²=6²
)²=6²
(x²+x)(x²+x+5)=36
x²+x=y⇒x²+x+5=y+5
y(y+5)=36
y²+5y-36=0
y²-4y+9y-36=0
y(y-4)+9(y-4)=0
(y-4)(y+9)=0
1) y-4=0
y=4
x²+x=4
x²+x-4=0
D=1+16=17
x=(-1±√17)/2
(-1+√17)/2>(-1+√16)/2=1,5>0
(-1-√17)/2<(-1-√16)/2=-2,5<-1
2) y+9=0
y=-9
x²+x=-9
x²+x+9=0
D=1-36=-35<0