Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=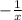
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= (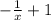 
) ' =
.
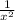3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=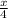
, к=1\4.
Найдем точку касания
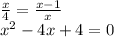
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х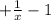
)' =
=1 -=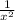
.
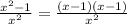у'=0 ,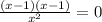 
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =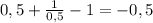
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5
решение на фотографии
Объяснение:
м. Крамера: находим 4 определителя.
1: это основная матрица
2: вместо первого столбика пишем числа, не относящиеся к переменным, - это -6, -5 и -2.
3: числа вместо 2 столбика
4: числа вместо 3 столбика
Далее по формулам также ищем значения самих переменных.
м Гаусса: меняются только строки, рядом с которыми написаны действия.
Допустим, 1я матрица, рядом с первой строкой I-III, значит из первой строки вычитаем числа третьей строки. В следующей матрице 1я строка полностью изменила. Где-то мы можем дорожать строки на числа и потом их прибавлять или отнимать, но мы их не меняем в следующей матрице. Должны получится единичная матрица, а числа за чертой, справа, это значения переменных.
х=3
у=0 решение системы.
Объяснение:
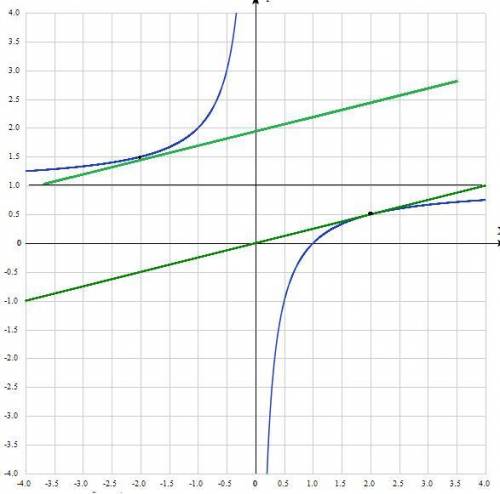
Решить систему уравнений графически это значит найти точку пересечения графиков этих функций (если она существует) и определить координаты этой точки пересечения, значения х и у , это и будет решение системы. Если точки пересечения нет, значит, система не имеет решения.
Построить графики. Уравнения линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем значение у, записываем в таблицу.
Для построения прямой достаточно двух точек, для точности определим три:
y=2х/3−2 y= −x+3
х -3 0 3 х -1 0 1
у -4 -2 0 у 4 3 2
Строим графики и определяем координаты точки пересечения.
Координаты точки пересечения можно вычислить. Для определения значения х приравняем правые части уравнений (левые равны) и вычислим значение х:
2х/3−2 = −x+3
Для избавления от дробного выражения умножим обе части уравнения на 3 (каждый член):
2х-6= -3х+9
2х+3х=9+6
5х=15
х=3
Теперь подставим найденное значение х в любое из двух данных уравнений и вычислим значение у:
у=(2*3)/3-2=2-2=0
у= -3+3=0
Координаты точки пересечения графиков функций (3; 0)
х=3
у=0, это решение системы.