![(y^{14}+x^{14})^2-(y^{14}-x^{14})^2-y^2x^2=\\\\=y^{28}+2x^{14}y^{14}+x^{28}-(y^{28}-2x^{14}y^{14}+x^{28})-x^2y^2=\\\\=4x^{14}y^{14}-x^2y^2=(2x^7y^7)^2-(xy)^2=\\\\=(2x^7y^7-xy)(2x^7y^7+xy)=xy\cdot xy\cdot (2x^6y^6-1)(2x^6y^6+1)=\\\\=x^2y^2\cdot (\sqrt2x^3y^3-1)(\sqrt2x^3y^3+1)(2x^6y^6+1)=\\\\=x^2y^2\, (\sqrt[6]2xy-1)(\sqrt[3]2x^2y^2+\sqrt[6]2xy+1) (\sqrt[6]2xy+1)(\sqrt[3]2x^2y^2-\sqrt[6]2xy+1)\times \\\\\times (\sqrt[3]2x^2y^2+1)(\sqrt[3]4x^4y^4-\sqrt[3]2x^2y^2+1)](/tpl/images/1090/1759/0c131.png)
Сначала построим график f(x)=2x+3.4
А теперь подумаем, что будет при взятии целой части числа.
Вот, допустим, f(x)=1 без взятия целой части, при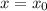 
, тогда при любом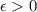 
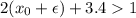, но при взятии целой части будет 1. Далее, при некотором 
, f(x)=2.
Но при любом 
При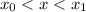 
идет прямая, в 
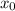точка не выколота, а вот в 
где f(x)=1 выколота, а вот где f(x)=2 не выколота.
И так далее.
При f(x)<0 все симметрично наоборот
На рисунке я постарался отметить все, что нужно. Синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
Пунктирами, по факту, отмечены разрывы функции. Это перпендикуляры к кусочкам графика
![Постройте график функции целой части числа f(x) = [2x + 3.4].](/tpl/images/0741/6343/5cb8e.jpg)
